算法笔记

算法部分

BFS与DFS

深度优先搜索（DFS）和广度优先搜索（BFS）是图遍历算法，也可以用于搜索树等数据结构。它们的主要区别在于遍历顺序和数据结构的不同。

深度优先搜索首先遍历一条路径直到它无法继续深入，然后回溯并尝试遍历另一条路径，重复此过程，直到所有路径都被遍历。可以使用递归或栈来实现深度优先搜索。

广度优先搜索从起始节点开始遍历，首先访问所有相邻节点，然后逐层向外扩展，直到找到目标节点或遍历完整个图。可以使用队列来实现广度优先搜索。

两者的主要区别在于遍历顺序和空间利用率。DFS会沿着一条路径尽可能远地探索，直到找到目标或无法继续。这通常导致DFS占用较少的空间，但可能导致它花费更长的时间，因为它可能需要搜索整个图或树。而BFS会逐层地遍历，可能需要更多的空间来存储每一层的节点，但是它通常会更快地找到目标节点。

一般来说，如果需要找到最短路径，或者需要遍历整个图或树，可以使用BFS。如果需要深入探索某一路径，或者需要找到任意一条路径，可以使用DFS。二叉树的遍历时间复杂度都是O(n)，其中n为树的节点数，因为需要访问树中的每个节点一次。

深度优先搜索的时间复杂度取决于遍历的节点数量。在最坏情况下，如果遍历整棵树，则时间复杂度为O(n)。在最好情况下，如果树是平衡的，时间复杂度为O(log n)。这是因为平衡二叉树的高度是对数级别的。在平均情况下，时间复杂度为O(n log n)。

广度优先搜索的时间复杂度同样取决于遍历的节点数量。在最坏情况下，如果遍历整棵树，则时间复杂度为O(n)。在最好情况下，如果树是满二叉树，时间复杂度为O(log n)。在平均情况下，时间复杂度为O(n)。

例题：

相同的树

题目部分

两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案

进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

Related Topics

数组

哈希表

1、双重循环，暴力破解

int *twoSum(int *nums, int numsSize, int target, int *returnSize) {
    for (int i = 0; i < numsSize; ++i) {
        for (int j = i + 1; j < numsSize; ++j) {
            if (nums[i] + nums[j] == target) {
                int *ret = malloc(sizeof(int) * 2);
                ret[0] = i;
                ret[1] = j;
                *returnSize = 2;
                return ret;
            }
        }
    }
    *returnSize = 0;
    return NULL;
}

2、哈希表，一层循环

struct hashTable {
    int key;
    int val;
    UT_hash_handle hh;
};

struct hashTable* hashtable;

struct hashTable* find(int ikey) {
    struct hashTable* tmp;
    HASH_FIND_INT(hashtable, &ikey, tmp);
    return tmp;
}

void insert(int ikey, int ival) {
    struct hashTable* it = find(ikey);
    if (it == NULL) {
        struct hashTable* tmp = malloc(sizeof(struct hashTable));
        tmp->key = ikey, tmp->val = ival;
        HASH_ADD_INT(hashtable, key, tmp);
    } else {
        it->val = ival;
    }
}

int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
    hashtable = NULL;
    for (int i = 0; i < numsSize; i++) {
        struct hashTable* it = find(target - nums[i]);
        if (it != NULL) {
            int* ret = malloc(sizeof(int) * 2);
            ret[0] = it->val, ret[1] = i;
            *returnSize = 2;
            return ret;
        }
        insert(nums[i], i);
    }
    *returnSize = 0;
    return NULL;
}

回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。

示例 1：

输入：x = 121
输出：true

示例 2：

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3：

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

提示：

-231 <= x <= 231 - 1

进阶：你能不将整数转为字符串来解决这个问题吗？

Related Topics

数学

数学解法

bool isPalindrome(int x) {
    double t = 0;
    double n = x;
    if (x < 0) {
        return false;
    } else {
        while (x) {
            int temp;
            temp = x % 10;
            t = t * 10 + temp;
            x /= 10;
        }
        return n == t;
    }
}

罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。

示例 1:

输入: s = "III"
输出: 3

示例 2:

输入: s = "IV"
输出: 4

示例 3:

输入: s = "IX"
输出: 9

示例 4:

输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= s.length <= 15
s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
题目数据保证 s 是一个有效的罗马数字，且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则，可以参考罗马数字 - Mathematics 。

Related Topics

哈希表

数学

字符串

1、暴力解法

int romanToInt(char * s){
    int n=strlen(s);
    int num=0,i=0,j=0,k=0;;
    int a[16];
    for(i=0;i<n;i++){
        switch(s[i]){
            case 'I':a[i]=1;break;
            case 'V':a[i]=5;break;
            case 'X':a[i]=10;break;
            case 'L':a[i]=50;break;
            case 'C':a[i]=100;break;
            case 'D':a[i]=500;break;
            default :a[i]=1000;break;
        }                           //按序存储字符对应10进制数字
    }
    for(i=0;i<n-1;i++){
        if(a[i]>=a[i+1]){
            num+=a[i];
        }
        else{
            num+=a[i+1]-a[i];
            i++;
        }
    }
    if(n==1)return a[0];            //一位罗马数情况
    if(a[n-1]<=a[n-2])
        num+=a[n-1];                    //末尾补位
    return num;
}

2、哈希表

char roman[7] = "IVXLCDM";
int data[7] = { 1, 5, 10, 50, 100, 500, 1000 };

int map(char c)
{
    int i = 0;
    for (i = 0; i < 7; i++) {
        if (roman[i] == c)
            break;
    }
    return i;
}

int romanToInt(char * s){
    int num = 0;

    for (int i = 0; i < strlen(s) - 1; i++) {
        if (map(s[i]) >= map(s[i + 1]))
            num += data[map(s[i])];
        else
            num -= data[map(s[i])];
    }
    num += data[map(s[strlen(s) - 1])];
    return num;
}

最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1：

输入：strs = ["flower","flow","flight"]
输出："fl"

示例 2：

输入：strs = ["dog","racecar","car"]
输出：""
解释：输入不存在公共前缀。

提示：

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

Related Topics

字符串

char *longestCommonPrefix(char **strs, int strsSize) {
    int a = strlen(strs[0]);
    int i = 0;
    char *ptr = strs[0];
    for (int j = 1; j < strsSize; j++) {
        for (i = 0; i < a; i++) {
            if (strs[j][i] == ptr[i]); else break;
        }
        a = i;

    }
    ptr[a] = '\0';
    return ptr;
}

有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

Related Topics

栈

字符串

1、暴力循环，字符串替换

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        length = len(s)
        if length < 2 or length % 2 != 0:
            if s == "":
                return True
            else:
                return False
        count = 2
        while count <= length / 2:
            s = s.replace("{}", "").replace("[]", "").replace("()", "")
            count += 1
        if s == "{}" or s == "[]" or s == "()" or s == "":
            return True
        else:
            return False

2、栈

from collections import deque

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        dict = {
            '{': '}',
            '[': ']',
            '(': ')',
            "1": "1"
        }
        if len(s) < 2 and len(s) % 2 != 0:
            if s == "":
                return True
            else:
                return False
        if s[0] in dict.values():
            return False
        stack = deque()
        stack.append("1")
        for i in s:
            if i in dict:
                stack.append(i)
            elif dict[stack.pop()] != i:
                return False
        return len(stack) == 1

3、栈，考虑其他情况

def isValid(s):
    """
    :type s: str
    :rtype: bool
    """
    dict = {
        ")": "(",
        "}": "{",
        "]": "["
    }
    stack = deque()
    for i in range(len(s)):
        # 如果右括号在前面
        if s[i] in dict:
            if len(stack) == 0:
                return False
            else:
                temp = stack.pop()
                if temp != dict[s[i]]:
                    return False
        else:
            stack.append(s[i])
    if len(stack) == 0:
        return True
    else:
        return False

合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

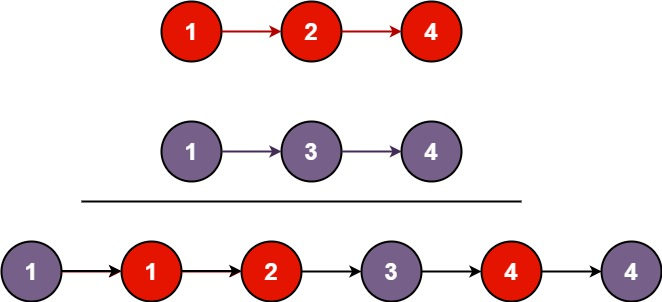
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

Related Topics

递归

链表

1、递归

                                         python
class Solution(object):
    def mergeTwoLists(self, list1, list2):
        """
        :type list1: Optional[ListNode]
        :type list2: Optional[ListNode]
        :rtype: Optional[ListNode]
        """
        if list1 and list2:
            if list1.val > list2.val: list1, list2 = list2, list1
            list1.next = self.mergeTwoLists(list1.next, list2)
        return list1 or list2

def mergeTwoLists(self, list1, list2):
    """
    :type list1: Optional[ListNode]
    :type list2: Optional[ListNode]
    :rtype: Optional[ListNode]
    """
    res = ListNode(-1)
    tmp = res
    while list1 and list2:
        if list1.val <= list2.val:
            tmp.next = list1
            list1 = list1.next
        else:
            tmp.next = list2
            list2 = list2.next
        tmp = tmp.next
    if list1:
        tmp.next = list1
    else:
        tmp.next = list2
    return res.next

删除有序数组中的重复项

给你一个 升序排列 的数组 nums ，请你** 原地** 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。

由于在某些语言中不能改变数组的长度，所以必须将结果放在数组nums的第一部分。更规范地说，如果在删除重复项之后有 k 个元素，那么 nums 的前 k 个元素应该保存最终结果。

将最终结果插入 nums 的前 k 个位置后返回 k 。

不要使用额外的空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列

Related Topics

数组

双指针

1、双重循环，暴力求解

class Solution(object):
    def removeDuplicates(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        for i in range(1, len(nums)):
            for j in range(i, len(nums)):
                if nums[i] == nums[i - 1]:
                    nums.pop(i)
        print(nums)
        return len(nums)

2、单层循环（冒泡）

def removeDuplicates(nums):

    """
    :type nums: List[int]
    :rtype: int
    """
    i = 1
    while (1):
        if i >= len(nums):
            break
        ptr1 = nums[i]
        ptr2 = nums[i - 1]
        if ptr1 == ptr2:
            nums.pop(i)
        else:
            i += 1
    return len(nums)

3、单层循环（插入）

def removeDuplicates(nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    i = 0
    while(1):
        if i >= len(nums):
            break
        temp = nums.pop(i)
        if temp in nums:
            pass
        else:
            nums.insert(i,temp)
            i += 1
    return len(nums)

4、双指针

def removeDuplicates(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    ptr1 = 0
    ptr2 = 1

    if len(nums) == 0:
        return 0
    while ptr2 < len(nums):
        if nums[ptr1] == nums[ptr2]:
            ptr2 += 1
        else:
            ptr1 += 1
            nums[ptr1] = nums[ptr2]
    nums = nums[0:ptr1]
    return ptr1 + 1

移除元素

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

Related Topics

数组

双指针

1、循环

def removeElement(self, nums, val):
    """
    :type nums: List[int]
    :type val: int
    :rtype: int
    """
    while val in nums:
        nums.pop(nums.index(val))
    return len(nums)

2、双指针

def removeElement(self, nums, val):
    """
    :type nums: List[int]
    :type val: int
    :rtype: int
    """
    fast = 0
    slow = 0
    while fast < len(nums):
        if nums[fast] != val:
            nums[slow] = nums[fast]
            slow += 1
        fast += 1
    return slow

最后一个单词的长度

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。

单词是指仅由字母组成、不包含任何空格字符的最大子字符串。

示例 1：

输入：s = "Hello World"
输出：5
解释：最后一个单词是“World”，长度为5。

示例 2：

输入：s = "   fly me   to   the moon  "
输出：4
解释：最后一个单词是“moon”，长度为4。

示例 3：

输入：s = "luffy is still joyboy"
输出：6
解释：最后一个单词是长度为6的“joyboy”。

提示：

1 <= s.length <= 104
s 仅有英文字母和空格 ' ' 组成
s 中至少存在一个单词

Related Topics

字符串

1、麻瓜解法，倒序遍历

def lengthOfLastWord(self, s):
    """
    :type s: str
    :rtype: int
    """
    rint = 0

    for i in range(len(s) - 1, -1, -1):
        if s[i] != " ":
            rint += 1
            if s[i - 1] == " ":
                break
    return rint

2、凤雏解法

def lengthOfLastWord(self, s):
    """
    :type s: str
    :rtype: int
    """
    return len(s.split()[-1])

加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位，数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]
解释：输入数组表示数字 123。

示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]
解释：输入数组表示数字 4321。

示例 3：

输入：digits = [0]
输出：[1]

提示：

1 <= digits.length <= 100
0 <= digits[i] <= 9

Related Topics

数组

数学

def plusOne(digits):
    """
    :type digits: List[int]
    :rtype: List[int]
    """
    digits[-1] += 1
    for i in range(len(digits) - 1, -1, -1):
        if digits[i] // 10 == 1 and i != 0:
            digits[i - 1] += 1

    for i in range(len(digits) - 1, -1, -1):
        if digits[i] >= 10:
            if i == 0:
                digits[i] = 0
                digits.insert(0,1)
                break
            digits[i] = 0
    return digits

二进制求和

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和。

示例 1：

输入:a = "11", b = "1"
输出："100"

示例 2：

输入：a = "1010", b = "1011"
输出："10101"

提示：

1 <= a.length, b.length <= 104
a 和 b 仅由字符 '0' 或 '1' 组成
字符串如果不是 "0" ，就不含前导零

Related Topics

位运算

数学

字符串

模拟

1、数组处理

def binary_sum(a, b):
    # 反转二进制字符串
    a = a[::-1]
    b = b[::-1]
    
    # 计算每一位的和
    res = ''
    carry = 0
    for i in range(max(len(a), len(b))):
        a_i = int(a[i]) if i < len(a) else 0
        b_i = int(b[i]) if i < len(b) else 0
        s = a_i + b_i + carry
        res += str(s % 2)
        carry = s // 2
    
    if carry != 0:
        res += str(carry)
    
    return res[::-1]

print(binary_sum('11', '1')) # 100

在这个程序中，我们定义了一个名为binary_sum的函数，它接收两个二进制字符串作为输入，并返回它们的和。在函数内部，我们首先将二进制字符串反转，以便按位处理。然后，我们遍历字符串的每一位，并计算它们的和。如果某一位的和大于2，它会产生进位，并将其加到下一位。最后，如果有进位，它会加到结果字符串的开头。

2、位运算

def addBinary(self, a, b):
    """
    :type a: str
    :type b: str
    :rtype: str
    """
    max_len = max(len(a), len(b))
    a = a.zfill(max_len)
    b = b.zfill(max_len)
    result = ''
    carry = 0
    for i in range(max_len - 1, -1, -1):
        if a[i] == '1' and b[i] == '1':
            result = ('1' if carry else '0') + result
            carry = 1
        elif a[i] == '0' and b[i] == '0':
            result = ('0' if not carry else '1') + result
            carry = 0
        else:
            result = ('0' if carry else '1') + result
    if carry:
        result = '1' + result
    return result

这个代码采用了位运算来优化二进制相加的过程，使得复杂度更低。

x的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

0 <= x <= 231 - 1

Related Topics

数学

二分查找

1、sqrt

def mySqrt(self, x):
    """
    :type x: int
    :rtype: int
    """
    return int(sqrt(x))

这段代码使用 Python 的 math 模块中的 sqrt 函数计算平方根。

2、二分查找

def mySqrt(self, x):
    """
    :type x: int
    :rtype: int
    """
    if x < 0:
        return None
    left, right = 0, x
    while left <= right:
        mid = (left + right) // 2
        if mid * mid <= x < (mid + 1) * (mid + 1):
            return mid
        elif x < mid * mid:
            right = mid - 1
        else:
            left = mid + 1
    return None

这段代码实现了对平方根的二分查找。我们通过设定左右边界来确定平方根所在的范围，并通过取中间值，判断它的平方是否大于等于给定数字，来逐渐缩小搜索范围。最终，如果找到的话，返回的是平方根的整数部分。

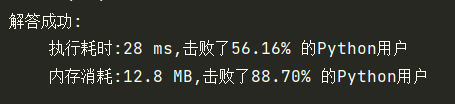
3、牛顿迭代

def mySqrt( x):
    """
    :type x: int
    :rtype: int
    """
    if x < 0:
        return None
    root = x
    precision = 0.00001
    while abs(root * root - x) > precision:
        root = (root + x / root) / 2
    return int(root)

在这段代码中，我们通过牛顿迭代公式：root = (root + x / root) / 2 不断地更新root的值，直到误差小于预期的精度。最终，我们将root的值向下取整，以获得整数部分的平方根。

4、牛顿迭代优化

使用二分查找：您可以使用二分查找来确定平方根的区间，然后使用牛顿迭代法来逼近结果。

def mySqrt(self, x):
    """
    :type x: int
    :rtype: int
    """
    if x < 0:
        return None
    left = 0
    right = x
    precision = 0.00001
    while left <= right:
        mid = (left + right) // 2
        if mid * mid <= x < (mid + 1) * (mid + 1):
            root = mid
            break
        elif mid * mid < x:
            left = mid + 1
        else:
            right = mid - 1
    root = left
    while abs(root * root - x) > precision:
        root = (root + x / root) / 2
    return int(root)

爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

Related Topics

记忆化搜索

数学

动态规划

1、迭代

def climbStairs(self, n):
    """
    :type n: int
    :rtype: int
    """
    if n == 1:
        return 1
    if n == 2:
        return 2
    return self.climbStairs(n - 1) + self.climbStairs(n - 2)

2、循环

def climbStairs(self, n):
    """
    :type n: int
    :rtype: int
    """
    if n == 1:
        return 1
    if n == 2:
        return 2
    a, b = 1, 2
    for i in range(2, n):
        a, b = b, a + b
    return b

3、动态规划

我们创建了一个数组dp来存储每个阶段的方案数。然后我们从第三个阶段开始循环，并使用前面两个阶段的结果来推导当前阶段的结果。最后，返回第n个阶段的结果即可。

def climbStairs(self, n):
    """
    :type n: int
    :rtype: int
    """
    if n == 1:
        return 1
    dp = [0] * (n + 1)
    dp[0] = 0
    dp[1] = 1
    dp[2] = 2
    for i in range(3, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]
    return dp[n]

删除排序链表中的重复元素

给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

示例 1：

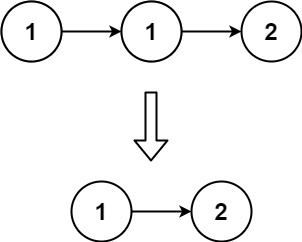
输入：head = [1,1,2]
输出：[1,2]

示例 2：

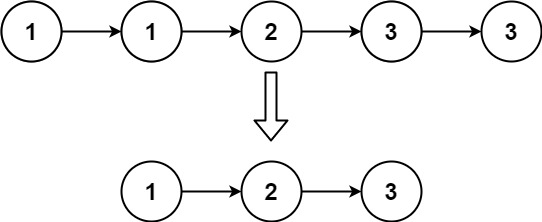
输入：head = [1,1,2,3,3]
输出：[1,2,3]

提示：

链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序排列

Related Topics

链表

python的链表

class ListNode(object):
     def __init__(self, val=0, next=None):
         self.val = val
         self.next = next

1、遍历，中间指针

def deleteDuplicates(self, head):
    """
    :type head: ListNode
    :rtype: ListNode
    """
    if not head:
        return head
    p = head
    while p is not None and p.next is not None:
        if p.val == p.next.val:
            p.next = p.next.next
        else:
            p = p.next
    return head

测试代码

# 创建一个有序链表 1->1->2->3->3
head = ListNode(1, ListNode(1, ListNode(2, ListNode(3, ListNode(3)))))
result = deleteDuplicates(head)
# 打印链表
while result is not None:
    print(result.val, end=" ")
    result = result.next
# 输出：1 2 3

2、字典加速删除过程

def deleteDuplicates(self, head):
    """
    :type head: ListNode
    :rtype: ListNode
    """
    if not head:
        return head
    val_dict = {head.val: True}

    p = head
    while p.next:
        if p.next.val in val_dict:
            p.next = p.next.next
        else:
            val_dict[p.next.val]=True
            p = p.next
    return head

3、集合加速，（python中集合的查找为O（1））字典的查找时间复杂度其实也为1

def deleteDuplicates(self, head):
    """
    :type head: ListNode
    :rtype: ListNode
    """
    if not head:
        return head
    val_set = set()
    val_set.add(head.val)

    p = head
    while p.next:
        if p.next.val in val_set:
            p.next = p.next.next
        else:
            val_set.add(p.next.val)
            p = p.next
    return head

合并两个有序数组

给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例 1：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

示例 2：

输入：nums1 = [1], m = 1, nums2 = [], n = 0
输出：[1]
解释：需要合并 [1] 和 [] 。
合并结果是 [1] 。

示例 3：

输入：nums1 = [0], m = 0, nums2 = [1], n = 1
输出：[1]
解释：需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意，因为 m = 0 ，所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。

提示：

nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109

进阶：你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗？

Related Topics

数组

双指针

排序

1、双指针

def merge(self, nums1, m, nums2, n):
    """
    :type nums1: List[int]
    :type m: int
    :type nums2: List[int]
    :type n: int
    :rtype: None Do not return anything, modify nums1 in-place instead.
    """
    i, j, k = m - 1, n - 1, m + n - 1
    while i >= 0 and j >= 0:
        if nums1[i] > nums2[j]:
            nums1[k] = nums1[i]
            i -= 1
        else:
            nums1[k] = nums2[j]
            j -= 1
        k -= 1

    while j >= 0 and k >= 0:
        nums1[k] = nums2[j]
        j -= 1
        k -= 1

二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

Related Topics

栈

树

深度优先搜索

二叉树

1、递归

def inorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    res = []
    if not root:
        return res
    self.inorder(root,res)
    return res

def inorder(self, node, res):
    if node.left:
        self.inorder(node.left, res)
    res.append(node.val)
    if node.right:
        self.inorder(node.right, res)

2、循环

def inorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    stack = []
    res = []
    while root or stack:
        while root:
            stack.append(root)
            root = root.left
        node = stack.pop()
        res.append(node.val)
        root = node.right
    return res

相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

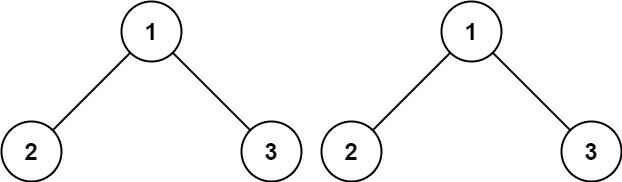
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

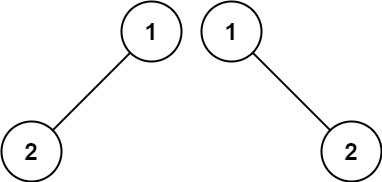
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

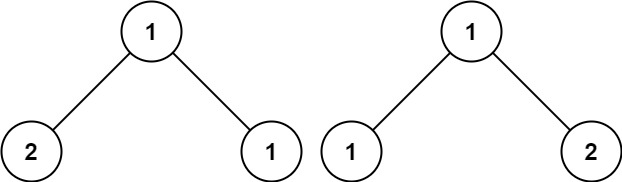
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

1、DFS

def isSameTree(self, p, q):
    """
    :type p: TreeNode
    :type q: TreeNode
    :rtype: bool
    """
    if not p and not q:
        return True
    if not p or not q:
        return False
    if p.val != q.val:
        return False
    return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)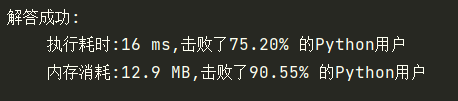

2、BFS

def isSameTree(self, p, q):
    """
    :type p: TreeNode
    :type q: TreeNode
    :rtype: bool
    """
    queue = [(p, q)]
    while queue:
        node1, node2 = queue.pop(0)
        if not node1 and not node2:
            continue
        if not node1 or not node2 or node1.val != node2.val:
            return False
        queue.append((node1.left, node2.left))
        queue.append((node1.right, node2.right))
    return True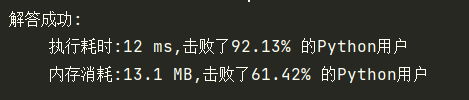

对称的二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

DFS

def isSymmetric(self, root):
    """
    :type root: TreeNode
    :rtype: bool
    """
    if root is None:
        return True
    return self.isMirror(root.left, root.right)

def isMirror(self, node1, node2):
    if node1 is None and node2 is None:
        return True
    if node1 is None or node2 is None:
        return False
    if node1.val != node2.val:
        return False
    return self.isMirror(node1.left, node2.right) and self.isMirror(node1.right, node2.left)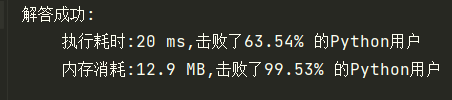

BFS

def isSymmetric(self, root):
    """
    :type root: TreeNode
    :rtype: bool
    """
    queue = [(root.left, root.right)]
    while queue:
        node1, node2 = queue.pop()
        if not node1 and not node2:
            continue
        if not node1 or not node2 or node1.val != node2.val:
            return False
        queue.append((node1.left, node2.right))
        queue.append((node1.right, node2.left))
    return True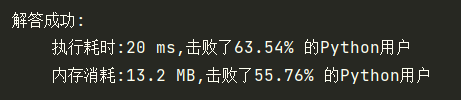

二叉树的深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

DFS

def maxDepth(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if root is None:
        return 0
    left = self.maxDepth(root.left)
    right = self.maxDepth(root.right)
    return max(left, right) + 1

BFS

def maxDepth(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if root is None:
        return 0
    queue = [root]
    depth = 0
    while queue:
        depth += 1
        level = len(queue)
        for i in range(level):
            node = queue.pop(0)
            if node.left is not None:
                queue.append(node.left)
            if node.right is not None:
                queue.append(node.right)
    return depth

将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列

Related Topics

树

二叉搜索树

数组

分治

二叉树

def sortedArrayToBST(self, nums):
    """
    :type nums: List[int]
    :rtype: TreeNode
    """
    if not nums:
        return None
    mid = len(nums) // 2
    root = TreeNode(nums[mid])
    root.left = self.sortedArrayToBST(nums[:mid])
    root.right = self.sortedArrayToBST(nums[mid + 1:])
    return root

寻找两个正序数组中的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

Related Topics

数组

二分查找

分治

def findMedianSortedArrays(self, nums1, nums2):
    """
    :type nums1: List[int]
    :type nums2: List[int]
    :rtype: float
    """
    m = len(nums1)
    n = len(nums2)
    res = [0] * (m+n)
    i, j, k = 0, 0, 0
    while i < m and j < n:
        if nums1[i] < nums2[j]:
            res[k] = nums1[i]
            i += 1
            k += 1
        else:
            res[k] = nums2[j]
            j += 1
            k += 1
    while i < m:
        res[k] = nums1[i]
        k += 1
        i += 1
    while j < n:
        res[k] = nums2[j]
        k += 1
        j += 1
    if (m + n) % 2 == 0:
        return (res[((m + n) // 2) - 1] + res[(m + n) // 2]) / 2.0
    else:
        return res[(m + n) // 2]

正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

1 <= s.length <= 20
1 <= p.length <= 30
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母，以及字符 . 和 *。
保证每次出现字符 * 时，前面都匹配到有效的字符

Related Topics

递归

字符串

动态规划

1、动态规划

假设字符串为 s，字符规律为 p，我们用 dp[i][j] 表示 s 的前 i 个字符是否能被 p 的前 j 个字符匹配。则有以下情况：

1. p[j] 是小写字母，即 p[j] == s[i]，则 dp[i][j] = dp[i-1][j-1]。
2. p[j] 是 '.'，可以匹配任意字符，即 dp[i][j] = dp[i-1][j-1]。
3. p[j] 是 '*'，可以匹配零个或多个前面的元素，有两种情况：
   - 如果 p[j-1] 和 s[i] 不匹配，则 dp[i][j] = dp[i][j-2]，表示直接忽略这个 '*' 和它前面的字符。
   - 如果 p[j-1] 和 s[i] 匹配，有三种情况：
     1. dp[i][j] = dp[i-1][j]，表示忽略掉 s 的第 i 个字符；
     2. dp[i][j] = dp[i][j-1]，表示把 '*' 当成单个字符，即匹配 s 的第 i 个字符；
     3. dp[i][j] = dp[i][j-2]，表示忽略掉 '*' 和它前面的字符。

最终的结果为 dp[len(s)][len(p)]。

def isMatch(self, s, p):
    """
    :type s: str
    :type p: str
    :rtype: bool
    """
    m, n = len(s), len(p)
    dp = [[False] * (n + 1) for _ in range(m + 1)]
    dp[0][0] = True

    for i in range(m + 1):
        for j in range(1, n + 1):
            if p[j - 1] == '*':
                dp[i][j] = dp[i][j - 2]
                if i > 0 and (s[i - 1] == p[j - 2] or p[j - 2] == "."):
                    dp[i][j] |= dp[i - 1][j]
            elif i > 0 and (s[i - 1] == p[j - 1] or p[j - 1] == '.'):
                dp[i][j] = dp[i - 1][j - 1]

    return dp[m][n]

2、递归

当 p 为空时，判断 s 是否为空，如果为空则匹配成功，否则匹配失败。
当 p 的长度为 1 时，分两种情况，如果 p 为字符 .，则只要 s 不为空，就匹配成功，否则匹配失败；如果 p 为其他字符，那么只要 s 的第一个字符和 p 相同，就匹配成功，否则匹配失败。
当 p长度大于 1 时，分两种情况：
1. 如果 p 的第二个字符不是 *，那么只要 s 不为空并且 s 的第一个字符和 p 的第一个字符相同，就递归地匹配 s[1:] 和 p[1:]。
2. 如果 p 的第二个字符是 *，那么有两种情况，一种是 * 匹配了 0 次，此时直接递归匹配 s 和 p[2:]，另一种是 * 匹配了 1 次或多次，此时如果 s 不为空并且 s 的第一个字符和 p 的第一个字符相同，就递归匹配 s[1:] 和 p。

def isMatch(self, s, p):
    """
    :type s: str
    :type p: str
    :rtype: bool
    """
    if not p:
        return not s
    match = bool(s) and p[0] in {s[0], '.'}
    if len(p) >= 2 and p[1] == '*':
        return self.isMatch(s, p[2:]) or (match and self.isMatch(s[1:], p))
    else:
        return match and self.isMatch(s[1:], p[1:])

平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

Related Topics

树

深度优先搜索

二叉树

DFS

def isBalanced(self, root):
    """
    :type root: TreeNode
    :rtype: bool
    """
    def height(root):
        if not root:
            return 0
        left_height = height(root.left)
        right_height = height(root.right)

        return max(left_height,right_height) + 1
    if not root:
        return True
    left_height = height(root.left)
    right_height = height(root.right)
    return abs(left_height - right_height) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)

BFS

1.定义一个队列，将根节点加入队列中。

2.进入循环，如果队列非空，执行以下操作：

1)弹出队列中的一个节点，判断该节点是否平衡。 2)如果该节点平衡，将其左右子节点加入队列。

3)如果该节点不平衡，直接返回 False。

3.如果队列为空，则返回 True。

def isBalanced(self, root):
    """
    :type root: TreeNode
    :rtype: bool
    """

    def get_depth(node):
        if not node:
            return 0
        return max(get_depth(node.left), get_depth(node.right)) + 1

    if not root:
        return True
    queue = [root]
    while queue:
        node = queue.pop(0)
        left_depth = get_depth(node.left)
        right_depth = get_depth(node.right)

        if abs(left_depth - right_depth) > 1:
            return False
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)
    return True

二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

DFS

首先判断根节点是否为空，如果是，则返回 0。如果根节点没有左右子节点，那么它的深度为 1。否则，分别求解左右子树的最小深度，并取较小值加 1，即为整棵树的最小深度。

需要注意的是，在递归求解左右子树的最小深度时，如果子树为空，应返回一个较大的值，以便在求最小值时不影响结果。例如，代码中使用了 float("inf") 表示正无穷。

def minDepth(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if not root:
        return 0
    if not root.left and not root.right:
        return 1

    left_depth = float('inf') if not root.left else self.minDepth(root.left)
    right_depth = float('inf') if not root.right else self.minDepth(root.right)

    return min(left_depth, right_depth) + 1

BFS

BFS 的基本思路是从根节点开始，一层一层地遍历，直到找到目标节点或遍历完所有节点。

具体实现时，可以使用队列来保存待遍历的节点。每次从队列中取出一个节点，将它的子节点加入队列中，直到找到目标节点或队列为空为止。在遍历过程中，还需要记录每个节点的深度，以便在找到目标节点时返回最小深度。

def minDepth(self, root):
    """
    :type root: TreeNode
    :rtype: int
    """
    if not root:
        return 0
    queue = [(root, 1)]
    while queue:
        node, depth = queue.pop(0)
        if not node.left and not node.right:
            return depth
        if node.left:
            queue.append((node.left, depth + 1))
        if node.right:
            queue.append((node.right, depth + 1))

queue 保存的是一个二元组 (node, depth)，表示节点和对应的深度。每次从队列头部取出一个节点，如果该节点是叶子节点，则返回其深度；否则将它的非空子节点加入队列中，并将深度加 1。如果队列为空但仍然没有找到叶子节点，则说明该树为空树，返回深度 0。

路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

树中节点的数目在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000

Related Topics

树

深度优先搜索

广度优先搜索

二叉树

DFS

def hasPathSum(self, root, targetSum):
    """
    :type root: TreeNode
    :type targetSum: int
    :rtype: bool
    """
    if not root:
        return False

    targetSum -= root.val

    if not root.left and not root.right:
        return targetSum == 0
    return self.hasPathSum(root.left, targetSum) or self.hasPathSum(root.right, targetSum)

这里使用了递归的方式实现深度优先搜索，函数参数 root 表示当前遍历到的节点，targetSum 表示目标和。如果当前节点为空，返回 False。否则，从目标和中减去当前节点的值，并判断当前节点是否为叶子节点。如果是叶子节点，判断目标和是否为零，如果是零，说明存在从根节点到叶子节点的路径，返回 True。否则返回 False。如果当前节点不是叶子节点，则递归遍历其左右子树，并将结果进行或运算，只要有一条路径满足条件即可。

BFS

使用 BFS 遍历二叉树。从根节点开始，对每个节点进行扩展，即将其左右子节点添加到队列中，同时更新当前路径的和。当遇到叶子节点时，检查路径和是否等于目标和，如果等于则返回 true，否则继续遍历下一个节点。如果队列为空仍然没有找到符合条件的路径，则返回 false。

def hasPathSum(self, root, targetSum):
    """
    :type root: TreeNode
    :type targetSum: int
    :rtype: bool
    """
    if not root:
        return False

    queue = [(root, root.val)]

    while queue:
        node, curr_num = queue.pop(0)
        if not node.left and not node.right:
            if curr_num == targetSum:
                return True
        if node.left:
            queue.append((node.left, curr_num + node.left.val))

        if node.right:
            queue.append((node.right, curr_num + node.right.val))
    return False

使用一个队列 queue 来存储当前待遍历的节点以及当前节点的路径和。我们首先将根节点和根节点的值加入队列中。然后对于每个节点，我们检查其是否为叶子节点，如果是，则检查当前路径和是否等于目标和，如果是，则返回 True。否则，我们将其左右子节点和路径和加入队列中，继续遍历下一个节点，直到队列为空或者找到符合条件的路径。

杨辉三角

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

提示:

1 <= numRows <= 30

Related Topics

数组

动态规划

def generate(self, numRows):
    """
    :type numRows: int
    :rtype: List[List[int]]
    """
    if numRows == 0:
        return []
    elif numRows == 1:
        return [[1]]
    elif numRows == 2:
        return [[1], [1, 1]]
    else:
        triangle = [[1], [1, 1]]
        for i in range(2, numRows):
            row = [1] * (i + 1)
            for j in range(1, i):
                row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j]
            triangle.append(row)
        return triangle

使用了一个二维数组 triangle 来存储杨辉三角中的每一行。我们首先处理特殊情况：当 numRows 为 0 时返回空数组，当 numRows 为 1 时返回一个只包含一个元素 1 的数组，当 numRows 为 2 时返回一个包含两个元素 1 的数组。

对于 numRows 大于 2 的情况，我们使用一个循环来生成杨辉三角的每一行。在循环中，我们首先创建一个长度为 i+1 的数组 row，并将其所有元素初始化为 1。然后，我们使用另一个循环遍历 row 中的每一个元素，计算其对应的值，即杨辉三角中的数值，并将其赋值给 row 中的相应位置。最后，我们将 row 添加到 triangle 中，完成一行的生成。

最后，我们返回 triangle，即杨辉三角的所有行。

杨辉三角II

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

输入: rowIndex = 3
输出: [1,3,3,1]

示例 2:

输入: rowIndex = 0
输出: [1]

示例 3:

输入: rowIndex = 1
输出: [1,1]

提示:

0 <= rowIndex <= 33

进阶：

你可以优化你的算法到 *O*(*rowIndex*) 空间复杂度吗？

Related Topics

数组

动态规划

def getRow(self, rowIndex):
    """
    :type rowIndex: int
    :rtype: List[int]
    """
    row = [1] * (rowIndex + 1)
    for i in range(1,rowIndex + 1):
        for j in range(i-1,0,-1):
            row[j] += row[j-1]
    return row

创建一个长度为 rowIndex+1 的数组 row 来保存每一行的数字。由于每行的数字只与上一行有关，我们可以使用递推公式 row[j] = row[j] + row[j-1] 来计算每行的数字。由于我们只需要返回第 rowIndex 行，因此可以在循环结束后直接返回 row 数组即可。

买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

1 <= prices.length <= 105
0 <= prices[i] <= 104

Related Topics

数组

动态规划

首先，定义状态 dp[i] 表示在第 i 天卖出股票所能获得的最大利润。我们需要在第 0 天买入，所以初始状态为 dp[0] = 0。

对于每一天 i，我们需要找到在前 i-1 天中股票价格的最小值 min_price。那么在第 i 天卖出股票所能获得的最大利润即为 prices[i] - min_price。如果这个利润比当前的最大利润 dp[i-1] 还要大，那么我们就更新 dp[i]。

最后，我们只需要遍历整个 dp 数组，找到最大的利润值即可。

def maxProfit(self, prices):
    """
    :type prices: List[int]
    :rtype: int
    """
    n = len(prices)
    if n <= 1:
        return 0
    dp = [0] * n
    min_price = prices[0]
    for i in range(1, n):
        min_price = min(min_price, prices[i - 1])
        dp[i] = max(dp[i - 1], prices[i] - min_price)
    return dp[-1]

验证回文串

如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。

字母和数字都属于字母数字字符。

给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。

示例 1：

输入: s = "A man, a plan, a canal: Panama"
输出：true
解释："amanaplanacanalpanama" 是回文串。

示例 2：

输入：s = "race a car"
输出：false
解释："raceacar" 不是回文串。

示例 3：

输入：s = " "
输出：true
解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。
由于空字符串正着反着读都一样，所以是回文串。

提示：

1 <= s.length <= 2 * 105
s 仅由可打印的 ASCII 字符组成

Related Topics

双指针

字符串

def isPalindrome(self, s):
    """
    :type s: str
    :rtype: bool
    """
    s = ''.join(c.lower() for c in s if c.isalnum())
    left, right = 0, len(s) - 1
    while left < right:
        if s[left] != s[right]:
            return False
        left += 1
        right -= 1
    return True

只出现一次的数字

给你一个非空整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1

示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：

输入：nums = [1]
输出：1

提示：

1 <= nums.length <= 3 * 104
-3 * 104 <= nums[i] <= 3 * 104
除了某个元素只出现一次以外，其余每个元素均出现两次。

Related Topics

位运算

数组

def singleNumber(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    res = 0
    for num in nums:
        res ^= num
    return res

可以使用异或运算来解决这个问题。异或运算有以下特点：

一个数和 0 做异或运算等于本身：a ⊕ 0 = a
一个数和本身做异或运算等于 0：a ⊕ a = 0
异或运算满足交换律和结合律：a ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ (a ⊕ a) = b ⊕ 0 = b

因此，如果我们对数组中的所有元素都进行异或运算，最后的结果就是那个只出现一次的元素，因为其他元素都出现了两次，异或之后就变成了 0。

环形链表

有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

进阶：你能用 O(1)（即，常量）内存解决此问题吗？

Related Topics

哈希表

链表

双指针

def hasCycle(self, head):
    """
    :type head: ListNode
    :rtype: bool
    """
    if not head or not head.next:
        return False
    slow = head
    fast = head.next
    while slow != fast:
        if not fast or not fast.next:
            return False
        slow = slow.next
        fast = fast.next.next
    return True

快慢指针的方法来判断链表中是否有环。快指针每次走两步，慢指针每次走一步，如果存在环，快指针最终会追上慢指针，否则快指针会到达链表的末尾

二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

输入：root = [1,2]
输出：[1,2]

示例 5：

输入：root = [1,null,2]
输出：[1,2]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

Related Topics

栈

树

深度优先搜索

二叉树

def preorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    res = []
    self.preorder(root, res)
    return res

def preorder(self, root, res):
    if not root:
        return
    res.append(root.val)
    self.preorder(root.left, res)
    self.preorder(root.right, res)

def preorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    if not root:
        return 
    stack,res = [root],[]
    while stack:
        node = stack.pop()
        res.append(node.val)
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)
    return res

二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

树中节点的数目在范围 [0, 100] 内
-100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

Related Topics

栈

树

深度优先搜索

二叉树

def postorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    if not root:
        return []
    left = self.postorderTraversal(root.left)
    right = self.postorderTraversal(root.right)
    return left + right + [root.val]

def postorderTraversal(self, root):
    """
    :type root: TreeNode
    :rtype: List[int]
    """
    if not root:
        return []
    stack = [root]
    res = []
    while stack:
        node = stack.pop()
        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)
        res.append(node.val)
    return res[::-1]

相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2：

输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

进阶：你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

Related Topics

哈希表

链表

双指针

def getIntersectionNode(self, headA, headB):
    """
    :type head1, head1: ListNode
    :rtype: ListNode
    """
    node_set = set()
    while headA:
        node_set.add(headA)
        headA = headA.next
    while headB:
        if headB in node_set:
            return headB
        headB = headB.next
    return None

def getIntersectionNode(self, headA, headB):
    """
    :type head1, head1: ListNode
    :rtype: ListNode
    """
    if not headA or not headB:
        return None
    p1, p2 = headA, headB
    while p1 != p2:
        p1 = p1.next if p1 else headB
        p2 = p2.next if p2 else headA
    return p1

Excel表名称

给你一个整数 columnNumber ，返回它在 Excel 表中相对应的列名称。

例如：

A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28 
...

示例 1：

输入：columnNumber = 1
输出："A"

示例 2：

输入：columnNumber = 28
输出："AB"

示例 3：

输入：columnNumber = 701
输出："ZY"

示例 4：

输入：columnNumber = 2147483647
输出："FXSHRXW"

提示：

1 <= columnNumber <= 231 - 1

Related Topics

数学

字符串

这道题是一道进制转换问题，从10进制转换成26进制，因为有A~Z，26个字母，所以可以把它们看成是26进制。

每次将 columnNumber 对 26 取余数，得到余数对应的字母，然后将 columnNumber 除以 26 取整。重复以上过程直到 columnNumber 为 0。最后将结果反转即可。

def convertToTitle(self, columnNumber):
    """
    :type columnNumber: int
    :rtype: str
    """
    res = []
    while columnNumber:
        columnNumber -= 1
        res.append(chr(columnNumber % 26 + ord('A')))
        columnNumber //= 26
    return ''.join(res[::-1])

多数元素

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3

示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：

n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

Related Topics

数组

哈希表

分治

计数

排序

def majorityElement(self, nums):
    """
    :type nums: List[int]
    :rtype: int
    """
    cand = nums[0]
    count = 1
    for i in range(1, len(nums)):
        if nums[i] == cand:
            count += 1
        else:
            count -= 1
        if count == 0:
            cand = nums[i]
            count = 1
    return cand

Excel表列序号

给你一个字符串 columnTitle ，表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。

例如：

A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28 
...

示例 1:

输入: columnTitle = "A"
输出: 1

示例 2:

输入: columnTitle = "AB"
输出: 28

示例 3:

输入: columnTitle = "ZY"
输出: 701

提示：

1 <= columnTitle.length <= 7
columnTitle 仅由大写英文组成
columnTitle 在范围 ["A", "FXSHRXW"] 内

Related Topics

数学

字符串

def titleToNumber(self, columnTitle):
    """
    :type columnTitle: str
    :rtype: int
    """
    res = 0
    for i in columnTitle:
        res = res * 26 + ord(i) - 65 + 1
    return res

两数相加

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

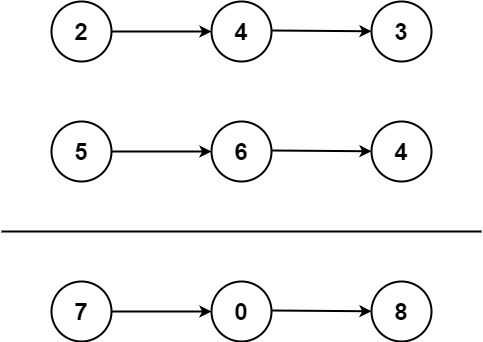
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零

Related Topics

递归

链表

数学

算法笔记

算法部分

BFS与DFS

题目部分

两数之和

回文数

罗马数字转整数

最长公共前缀

有效的括号

合并两个有序链表

删除有序数组中的重复项

移除元素

最后一个单词的长度

加一

二进制求和

x的平方根

爬楼梯

删除排序链表中的重复元素

合并两个有序数组

二叉树的中序遍历

相同的树

对称的二叉树

二叉树的深度

将有序数组转换为二叉搜索树

寻找两个正序数组中的中位数

正则表达式匹配

平衡二叉树

二叉树的最小深度

路径总和

杨辉三角

杨辉三角II

买卖股票的最佳时机

验证回文串

只出现一次的数字

环形链表

二叉树的前序遍历

二叉树的后序遍历

相交链表

Excel表名称

多数元素

Excel表列序号

两数相加

你的赏识是我前进的动力