高等数学学习笔记
数学公式显示错误时,可刷新界面。
函数
在高等数学里,微积分无疑是极为重要的,但是如果没有函数去研究微积分,这其实很没有意义,在微积分的世界里,函数在参与排行榜绝对排行第一。
函数概念
函数是什么?在很多教材或者课外读本上都有规范或者是特殊的定义,我更加喜欢普林斯顿微积分的描述,函数是将一个对象转化为另一个对象的规则。
这听起来似乎和工厂、程序之类的概念类似,而且一点也不数学。
首先要说的是,函数是一个变换规则,例如f(x),说 “f (x) 是 一个函数”其实是不正确的, 应该说 “f 是一个函数“。
其次,每一个函数都有输入与输出,对于输入而言,应当是有效的,如同f(x) = x-2这样函数表达式,如果我们输入一个“人”,这显然没有任何意义。
然后,对于函数而言,如果只有输入而没有输出就会显得毫无意义,因此,一个函数必须给每一个有效的输入指定唯一的输出。
区间表示
我们在说明输入的有效与输出的范围时,会使用定义域与值域,但实际上,在普林斯顿里,还有上域与下域的说法。在描述这样的范围时,区间的表示会让我们做的更好。
我们约定 [a, b] 是指从 a 到 b 端点间的所有实数, 包括 a 和 b。类似这样的称作闭区间。 如果你不想包括端点, 把方括号变为圆括号就行了,这样的成为开区间,当然如果你想包含一边又不要一边的端点,你就可以一边方括号一边圆括号,这样的就是半开区间。
求定义域
很多时候,函数的定义会包括定义域,但是有些时候,函数的定义域没有给出,通常,定义域包含实数集R以及尽可能多的部分。
但是在某些时候,例如负数的平方根,这就会出现问题,它的定义域一定是非负数。
还有一些常见的情况:
分数的分母不能为0。(tan 90不成立)
不能取一个负数的偶次方根。
不能取到一个负数或者是0的对数。
求值域
如果可以,我们将一个函数画出图像后,我们会发现,无论是定义域还是值域似乎都变得容易起来,我们甚至还可以从图像上观察出最值,变化趋势等等很多的内容。
函数的值域,在我们画出图像后,我们不妨假设此此刻有左右的光束射入光束,而后在y轴上留上影子,这个影子的并集就是值域。
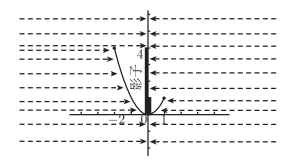
感谢普林斯顿,在看到这一幅图的时候,想必你对某些教材上关于函数与映射的描述也能清晰几分。
检验函数成立
上面的例子里,我们用横线来模拟光照得到了值域,如果我们使用竖线呐?
这很帮助我们确定函数是否成立。
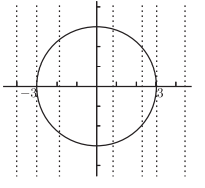
如图的画,我们发现对于某些竖线,圆与它有超过一个以上的交点,这就违反了函数中,一个输入得到唯一输出的原则。
反函数
对于函数而言,你给一个输入就可以得到一个输出,前提是在定义域与值域之内。如果我们把过程倒过来,你选一个输出,那么说明样的输入能得到这个输出呐?
这其实就是一个逆转变换的过程,从输出出发,发现一个新的函数,这个函数就是原函数的反函数。f-1这就是他的写法。
对于这样的情形有一些总结:
反函数的定义域和原函数的值域相同.
原函数的定义域和反函数的值域相同。
反函数更加像是原函数的撤销按钮,从x出发你可以得到y,从y出发,你可以逆转这个过程,重新得到x。
但是并不是所有的原函数都可以得到反函数的。
我们知道函数成立的基本条件就是,一个输入得到一个唯一确定的输出。
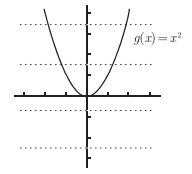
如上的函数,我们通过他的图像不难发现,一个输出对应了两个输入。
如果对于他的定义域不加以限制,那么反函数就会出现一个输入对应两个输出的情况。
对于什么样的函数能得到反函数,可以使用水平线的方式检验。
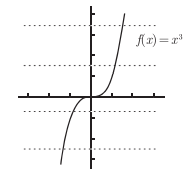
如上,每一条水平线与函数至多只有一个交点,那么这样的函数就可以得到反函数。
求反函数
这看起来似乎很困难,但其实只要得到表达式,我们根据表达式,直接解出x就好了。
在图像上,反函数其实类似于镜面反射,在坐标轴中,这个镜面指的就是y=x这一第一、第三象限的分界线。
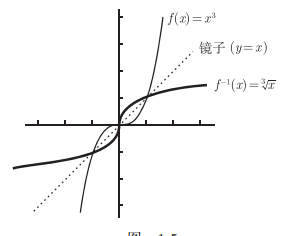
限制定义域
这是为了没有通过水平线检验的函数准备的,通过限制定义域的方式,相当于擦去了一部分图像,来得到反函数。
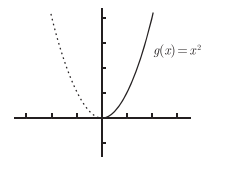
但是要注意原函数限制了定义域,那么反函数的值域也就得到了限制。
反函数的反函数
既然反函数是对原函数的撤销,那么反函数的反函数其实就是原函数,但是要注意定义域。
复合函数
有一个表达式为 g(x) = x2 的函数g。 你可以将 x 替换成任何使函数有意义的对象,这样的复合函数可能包含两个或者更多的基本函数。
复合函数有一个很简单也很重要的例子,将函数f(x)=x2和函数g(x)=x-a(a是常数)进行复合。这时得到的函数在形状上看起来与函数f是一样的,只不过是原函数图像向右平移了a个单位。(假设,向左平移3个单位与向右平移-3个单位是一样的。)
奇函数和偶函数
有的函数在图像上具有对称的特性,这很方便对他们进行讨论。
偶函数的图像关于y轴对称,而奇函数关于原点有180o对称
研究函数
$$
y = x^n
$$
,我们发现当n为奇数时,函数图像虽然各不相同,但是总是关于原点对称,n为偶数时,函数图像总是关于y轴对称。
线性函数
形如,mx+b的函数就是线性函数,这个名字的来源就是他们的图像是直线,直线的斜率是m,b是y轴的截距。
常见函数
1、多项式(二次函数)
$$
f(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0
$$
2、有理函数
有理函数是指一个多项式除以另一个多项式的形式。
$$
f(x) = \frac{p(x)}{q(x)}
$$
有理函数的定义域由分母确定,即在分母等于 0 的点处有定义域限制。
有理函数的图像可能包含垂直渐近线和水平渐近线,因为在某些点上有理函数可能无限接近于某个数值或无限增长。
指数和对数函数
$$
f(x) = a^x
$$
数函数的图像通常是一个增长或衰减非常快的曲线。当 a>1 时,函数增长得非常快;当 0<a<1 时,函数衰减得非常快。
对数函数是指数函数的反函数。
$$
f(x) = \log_a x
$$
对数函数的定义域是
$$
(0, \infty)
$$
,值域是
$$
(-\infty, \infty)
$$
。对数函数的图像通常是一个缓慢增长或下降的曲线,且它与指数函数的图像在 y=x 的直线上对称。
需要注意的是,当底数 a 等于自然常数
$$
e \approx 2.71828
$$
时,指数函数
$$
e^x
$$
称为自然指数函数,对数函数
$$
\ln x
$$
称为自然对数函数。
带有绝对值的函数
$$
f(x) = |x|
$$
它表示的是 x 的绝对值,即无论 x 是正数还是负数,它的函数值总是非负数。对于正数 x,|x| = x,对于负数 x,|x| = -x。
有一个看待绝对值函数的方法是,他表示数轴上0和x之间的距离。
绝对值函数的图像是一条 V 形的曲线,过原点,并且它在 x 轴左侧和右侧的斜率分别为 -1 和 1。
需要注意的是,绝对值函数并不是光滑函数,即它在 x=0 处不可导。
三角函数
弧度是一个角度的度量单位,它是一种用弧长来度量角度大小的方式。
在一个圆的周长上选取一个弧段,如果这个弧段长度等于该圆半径的长度,那么这个弧段所对的圆心角就称为一个弧度。通常用符号
$$
\theta
$$
来表示一个角度的弧度值。
由于圆的周长是
$$
2\pi r
$$
,所以圆心角度数为
$$
360^\circ
$$
的弧长为 $2\pi r$,所以一个圆心角度数为
$$
360^\circ
$$
的角对应的弧度值为
$$
2\pi
$$
。因此,我们可以用以下公式将角度转换为弧度:
$$
\theta = \frac{\pi}{180} \times \text{度数}
$$
类似地,我们也可以用以下公式将弧度转换为角度:
$$
\text{度数} = \frac{180}{\pi} \times \theta
$$
微积分概念
微积分到底是什么?
微分与积分的关系是什么?
回想高数的学习历程,最后发现好像对于微积分来说,除了课本上习题册上的题目,其他的我就完全不知道了,甚至于再过些时间,这些题目我也做不了了。
我的看法是,当我们学习或者是掌握了一门学科或者是一门技术之后,我们应当对它有提纲挈领的认知。
微积分关心的是瞬时的情况。
首先,让我们来看一个实际例子,我们用最常见的时间、速度、路程函数。
假设,一辆汽车,当然也可以是一个人或者你想要假设的任何东西,现在它以20km每小时的速度向前行驶,三个小时过后。让我们看看时间与速度、时间与路程的关系。
时间与速度:
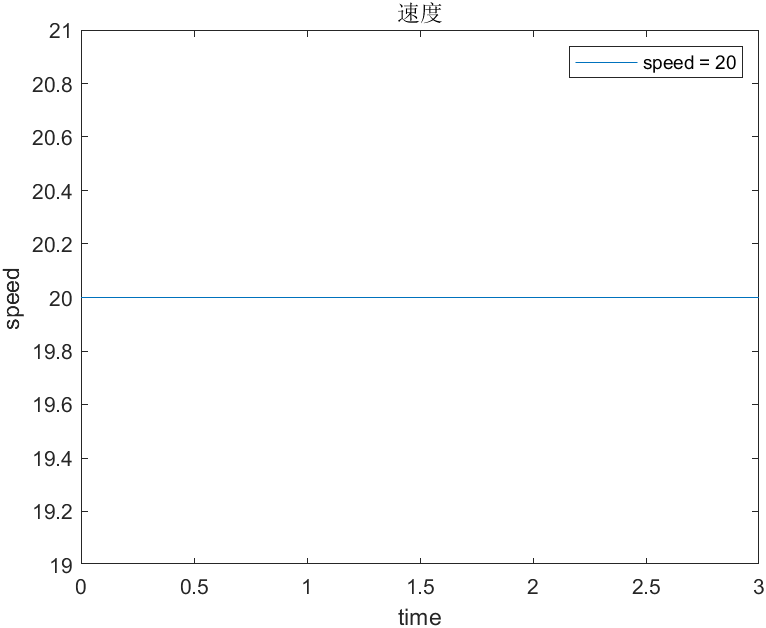
时间与路程:
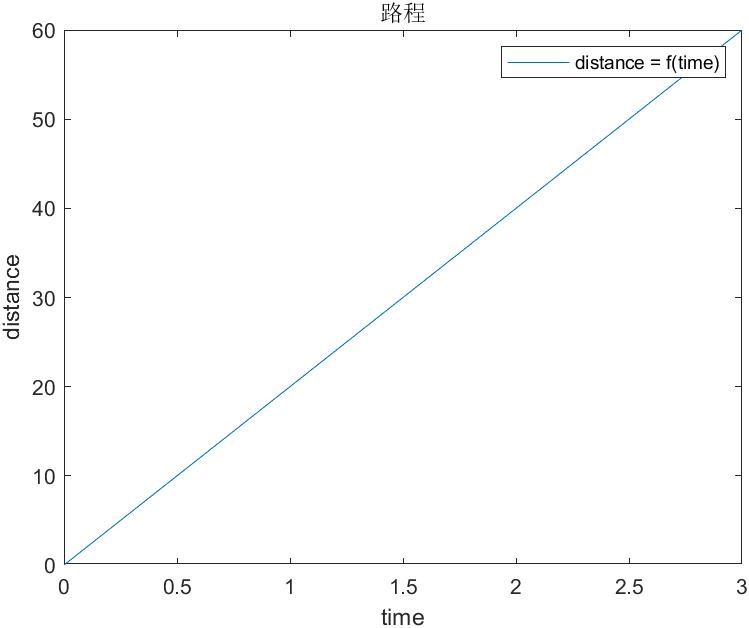
如上,我们得到了时间与速度的关系,时间与路程的关系。
如果我们再试着想象一下,速度如果不是匀速?
时间与速度:
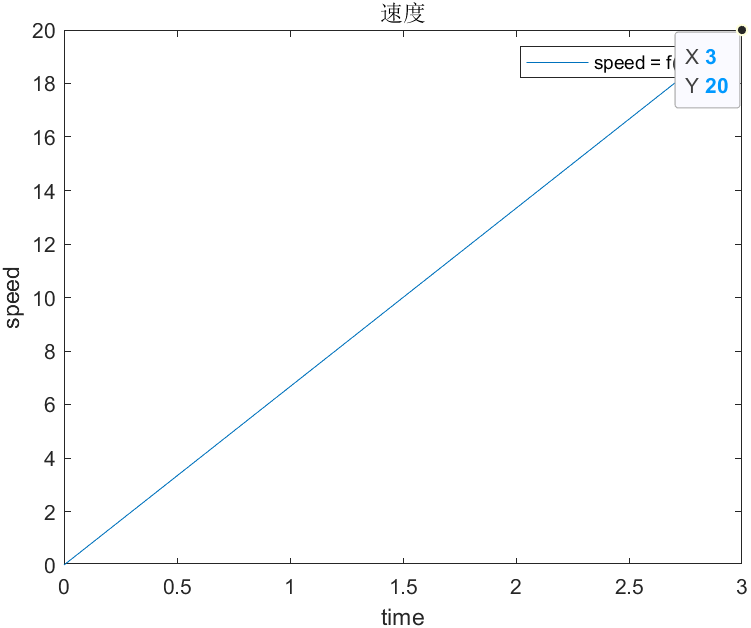
时间与路程:
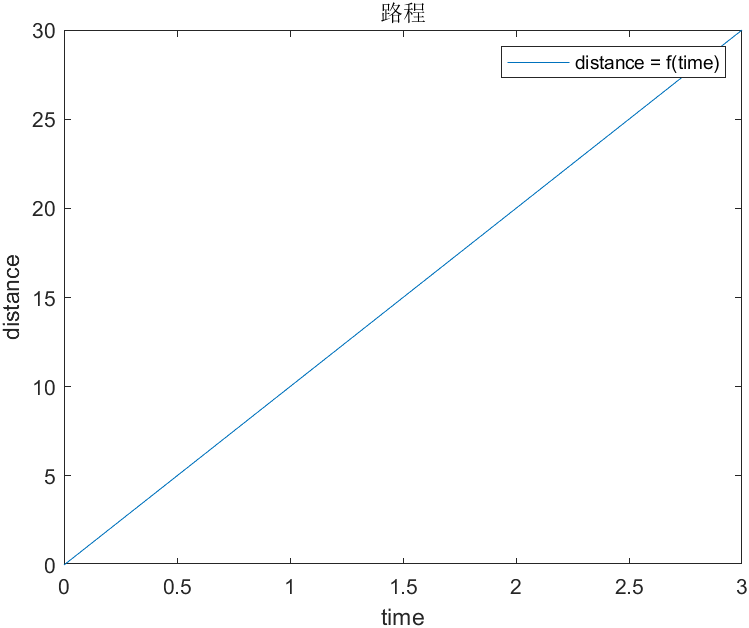
虽然在图像上,好像两个路程函数看起来差不多,但是从y轴,也就是distance的值上,我们明显的感觉到,因为速度的变化,路程函数发生了变化。
同样的,如何我们改变路程函数,那么速度函数也会发生改变。
而微积分研究的本质上就是两个函数的关系。
其中从速度到路程,是积分的过程,而从路程到速度,是微分的过程。
或者说,我们再举一个例子。
当你出生的时候,你的年龄为0岁,这时候你大概有10公斤,当然我也不知道,瞎编了一个数字。而后当你10岁的时候,你已经37公斤了,当你18岁的时候,你已经49公斤了,而后等你30岁的时候,你已经59公斤了,此时你来到你人生体重最高点,再往后,50岁的时候,你就只有58公斤了,一直到62岁,你就只有52公斤了。
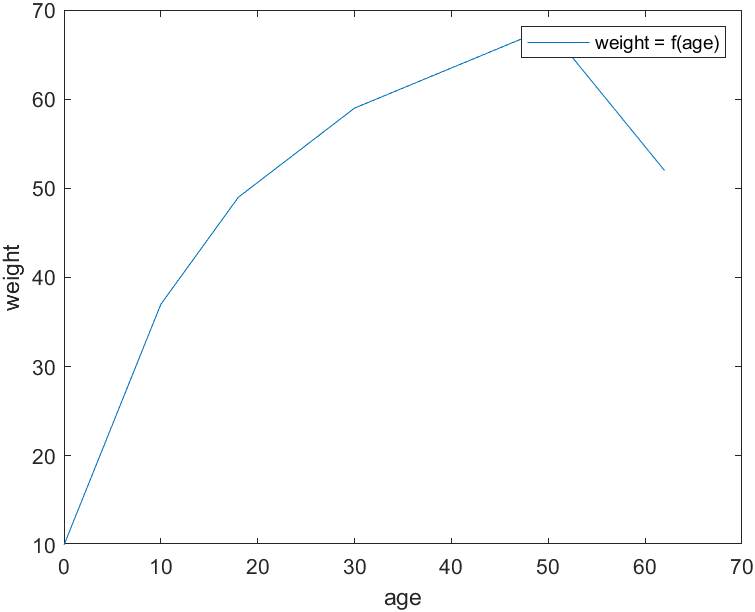
如图,简单的把以上提到的点描成这样的图。
那么?新的问题来了,能否根据它得出体重的增长率呐?
导数
关于导数,首先应该区分开一个概念。
那就是可导与可微,前者表示的是变化率的极限,而后者表示的是局部线性化。
导数和微分是紧密相关的概念,但并不是完全一样的概念。导数是函数在某一点处的变化率,也就是函数值的增量与自变量值的增量之比,它表示的是函数在某一点处的瞬时变化率。而微分则是对函数进行局部线性近似的一种方法,它用切线来近似曲线,从而得到函数在某一点处的变化情况。
可以说,导数是微分的结果,也就是函数在某一点处的局部线性近似斜率。微分的本质是用线性函数逼近非线性函数,即把非线性函数局部线性化,这样就可以利用线性函数的性质来分析非线性函数的性质。
斜率,如果你还记得他,那么再好不过。
在生活中,我们用斜率来表示倾斜角度,回到函数图像上,其实他也同样如此。
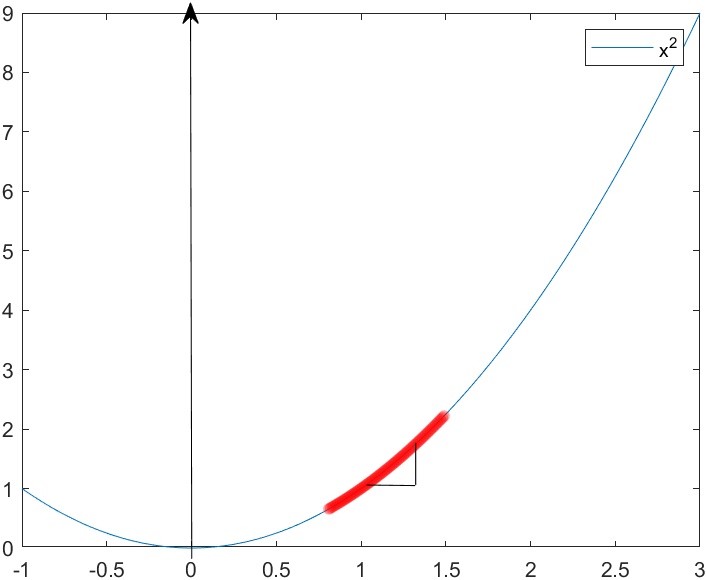
如图,这是函数x2的函数图像。
这样的曲线,我们是如何求斜率的呐?
如果这不是曲线,而是直线,例如y = 2x呢。
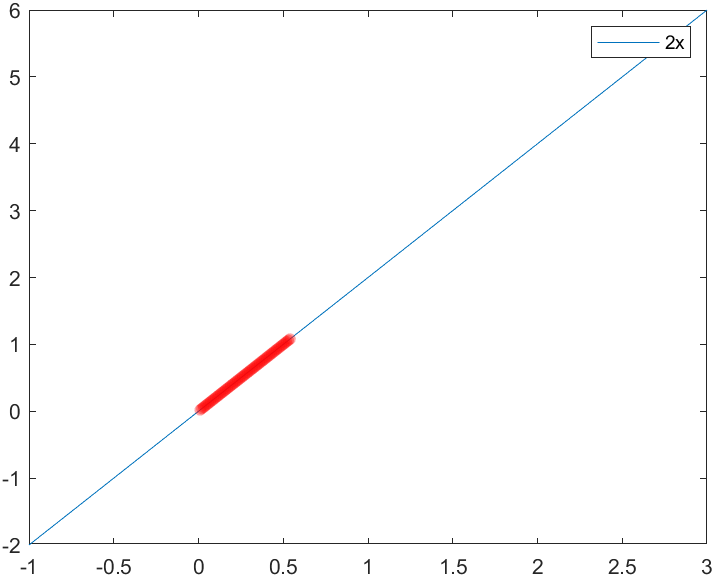
我们直接利用垂直距离差比上水平距离差,就可以解出斜率。
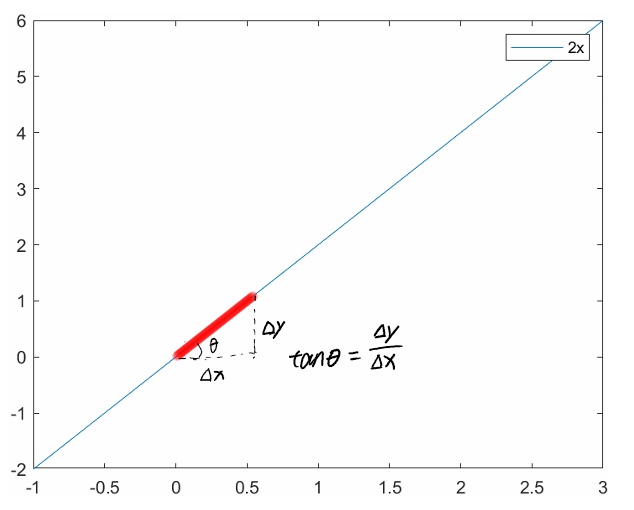
这时候,∆y与∆x的比值,也就是θ角的正切就是斜率。
再次回到曲线的问题,只看x轴右半轴,假设这是一个表示路程的函数,那么在这里我们就可以得到任意的时间段内,这个车或者是其他的什么东西在这个时间段内的平均速度,这很简单,还未涉及微积分。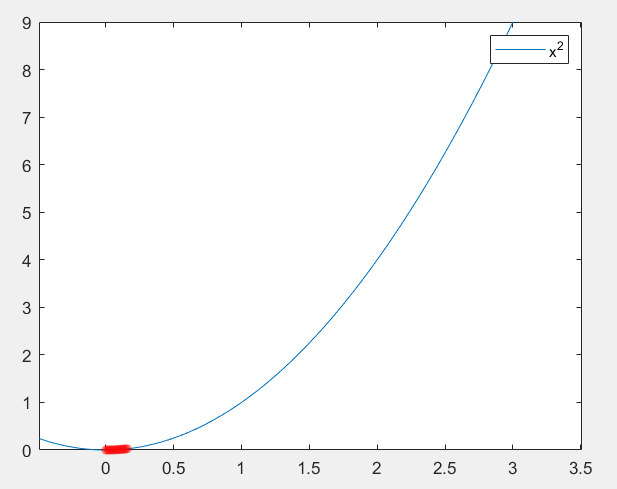
那么这段时间的速度,我们就应该用路程差比时间差,反应在图像中,就是垂直距离差比水平距离差。
微积分只关心瞬时情况,不如我就从x = 0这一点开始,当x=0的时候,这一点的斜率是怎么样的?
x = 0,y = 0.这是原点,可以发现此时虽然曲线依然在上升,但是有点像是刚刚起步,此时速度为0,因此这一点斜率为0,曲线水平。
实际上,求最低点也是微积分的主要应用之一,通过求斜率为0,可以求出最低点,这一点不上升也不下降,斜率为0。
这时,我们可以选一个离原点距离极小的点,标记为∆x,这个∆单纯的就是为了表示“小”的意思,他代表一个极小极小的变化。那么这时候从原点到∆x这一小段的平均速度是多少?平均斜率?
水平距离是∆x,曲线是简单的x2,垂直距离很明显。
平均斜率还是垂直比水平。即∆y / ∆x
虽然∆x已经非常非常小了,但是这里他依旧是平均值,我想让他减少到0,取极限,让这一段不断的减小,从而无限接近某个瞬间的情况,这样就能得到斜率,这样就能得到0点处的斜率。
这里的情形很简单,可以看到∆x2 / ∆x的比值∆x会非常的小。因此平均斜率非常之小,沿着这种逐渐变小的思路,我将得到x = 0处的瞬时斜率。
让∆x逐渐减小,最后到0。
相当于行驶从静止开始,然后慢慢加速,这时候斜率很明显就不是0了。
来看一下任意点的斜率。
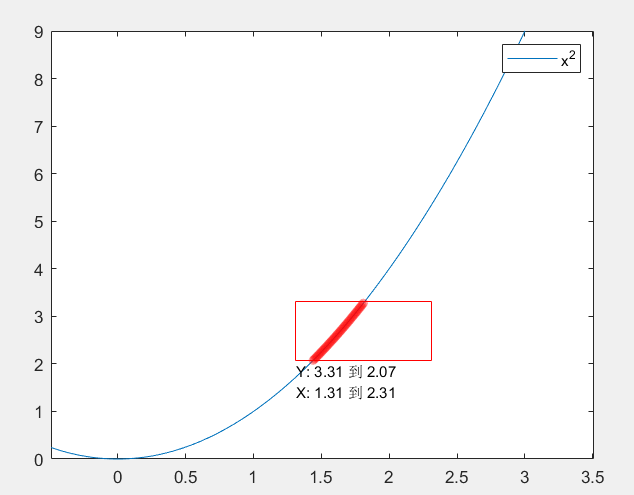
微积分的要义,取一小段距离∆x,移动到x+∆x处,这样的y就会移动到曲线上另外一点,这一点的值为y + ∆y或者是(x+∆x)2,因为此时的曲线还是y = x2
此时的水平距离与垂直距离各自是∆x与∆y。
此时的∆y 比 ∆x应当为 ((x+∆x)2 - x2) / ∆x
继续进行代数运算,我们得到了2x+∆x的结果,也就是说,此时的∆y比∆x的结果为2x + ∆x。
当然,到目前为止,这依然是小范围的平均值,还不是瞬时的情形。
当微积分开始介入,dy / dx。
如果说前面是小 / 小,那么这就是极小 / 极小。
这里的d,小的可以说已经无法分辨,小的已经无法把dy或者dx作为分开距离来考虑。
要注意,这里其实不是真正的除法了,因为在除法中,是不允许0 / 0的。而此处的0 / 0其实就是上面这种情况(∆y / ∆x)的极限。
这就是从代数走进微积分最关键的一步,这就得到了某一点上的瞬时情形。
再看上面的结论,取∆x趋近于0,那么结果就是2x。
因此最终的结论是,导数为2x。
因此这就是我们所说的函数二,也就是斜率函数,或者说是速度函数。
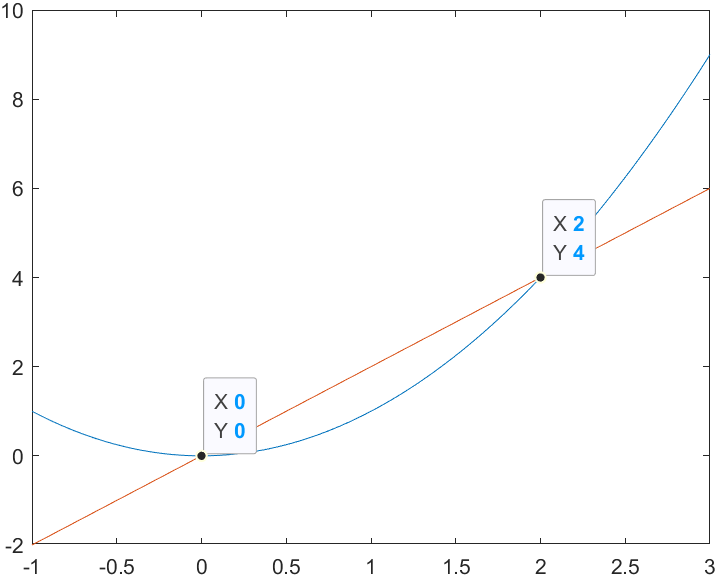
再来看,此时如果我们取(1,1)与(2,4)这两个点来讨论斜率。
那么自然而然的就会得到,斜率为3.
但实际上,这只是一条弦,这里跳了一大步。
我们在讨论∆x时,只是前进了一小步,更别说趋近于0时的dx了,这就成了无限小的一步。
因此实际的斜率,可以认为是过某一点的切线。
那么这一点的斜率,实际上就是把x =1 代入到我们的斜率函数也就是2x里。
因为我们可以通过斜率判断函数图像的走向,当斜率为负时,函数呈现下降趋势,当斜率很大的时候,函数图像往往更加陡峭,反之,当斜率为正时,函数图像成上升趋势,斜率很小的时候,函数图像更加平滑。
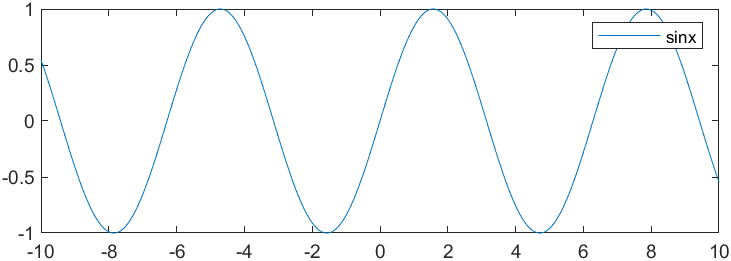
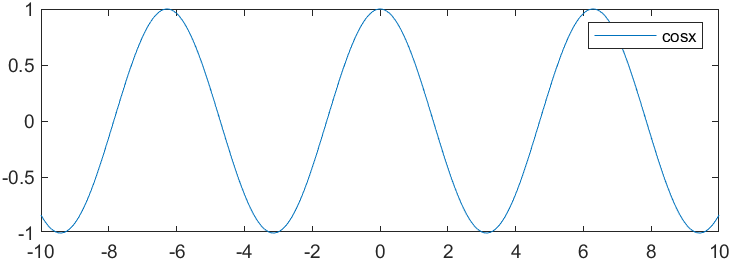
这是sinx与cosx的函数图像,当然可能坐标轴有些陌生。
sinx的导数是cosx,那么比较这两个图像,增长,下降,快,慢,极大值,极小值。这些都体现了导数的重要性和实用性。
二阶导数与极值
二阶导数:也就是导数的导数。
在实际中,很少提到导数的导数,或者说更加高阶的导数,但是二阶导数对于处理极大、极小值时作用很大。
我们经常需要定位极值点,并且判断是极大值还是极小值。
定位极值点是一阶导数的职责,一阶导数为0的点就是极值点,如果函数存在极大值或者是极小值,要找到这个极值点的位置,就可以通过导数=0来寻找,此时函数图像趋于水平,根据它向下还是向上弯曲,得到极大值或者是极小值。
而判断极值点是极大值还是极小值就是二阶导数的职责了。
二阶导数表明,函数朝上还是朝下弯曲。
原函数,导函数,二阶导函数,现在的函数组就扩充为三个。
回到实际问题,依旧是路程,时间,速度的关系,二阶导函数其实表示的就是加速度。
我们知道路程求速度,只需要求导数就可以了,现在我们要求速度的导数,也就是二阶导数,加速度,也就是速度的变化率,加速或者减速的率。
先来看看x2的原函数,导函数与二阶导函数。
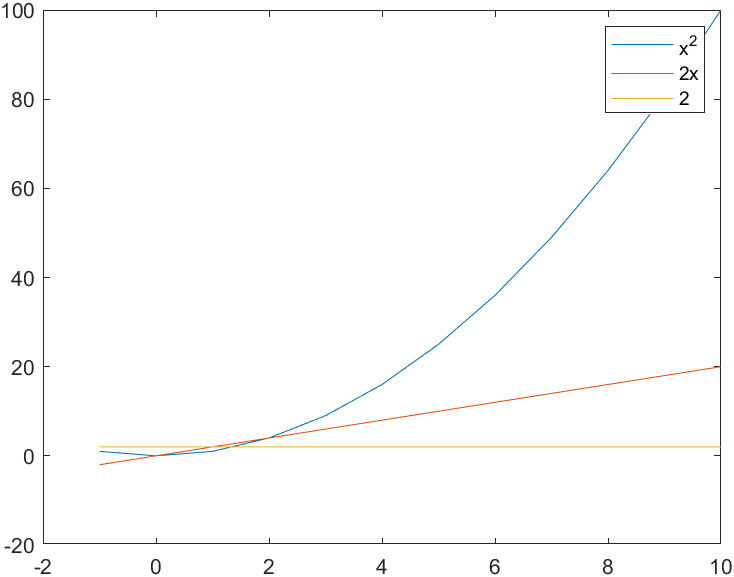
依旧是x2,表示函数高度,2x表示斜率,而2表示二阶导数,表示弯曲性,这表明斜率正在逐渐增加,函数图像向上弯曲。
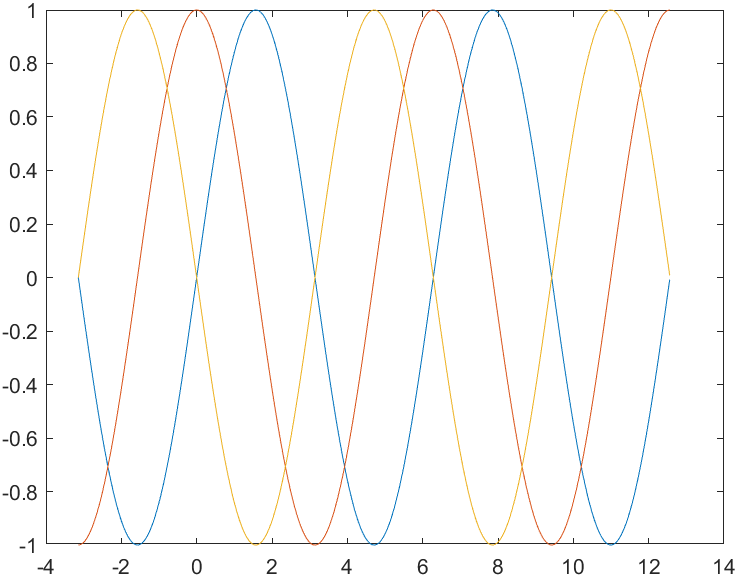
在看看sinx的原函数、导函数与二阶导函数的图像。
事实上,图像上包含的信息可比说的信息多的多了,在0-π/2区间内,我们发现,sinx的二阶导数小于0的,也就是说此时的原函数向下弯曲,导函数应当呈现下降趋势。
引入“凹凸”的概念,事实上,我个人觉得,向上弯曲与向下弯曲的描述比凹凸更好。
sinx就是一个很经典的例子,在图像中,我们发现0-π/2区间内,即使图像向下弯曲,但是同样呈现在不断增长。
原函数 导函数 二阶导函数的关系也明了了。
二阶导函数大于零,表示导函数上升,毕竟对于导函数来说,二阶导数就是它的导数,原函数向上弯曲,反之。
x = π时,二阶导数变号了,而此时原函数开始向上弯曲。这个点就是拐点,二阶导数为0的点。
拐点意味着,二阶导数穿过0,即原函数的图像弯曲性发生改变。这一点在图像里很重要,当然没有极大值和极小值那么显眼。
y = x3 - x2
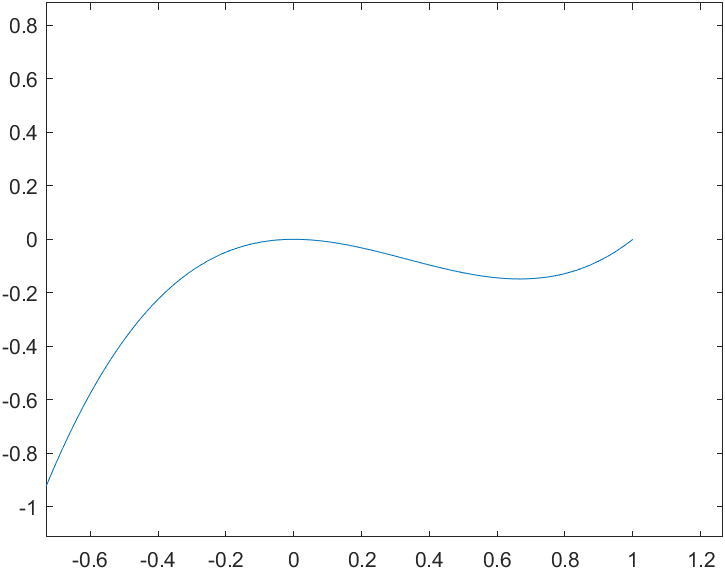
首先求导:3x2-2x ,二阶导数:6x -2
极值点:令一阶导数为0,将所有的极值点一网打尽,之后通过二阶导数判断极大值与极小值。
那些点上,函数停止住了,既不上升,也不下降
在图像上,很容易找到,代数也很容易求出,一元二次方程的两个解。
不同的是,看图像很容易得到极大值与极小值,之所以不是最值,是因为图像明显的,会在x趋近于正无穷时,趋近于正无穷,因为该点只在其附近(领域内)是最大值,因此称作极大值或者局部最大值。极大值处会有什么性质?
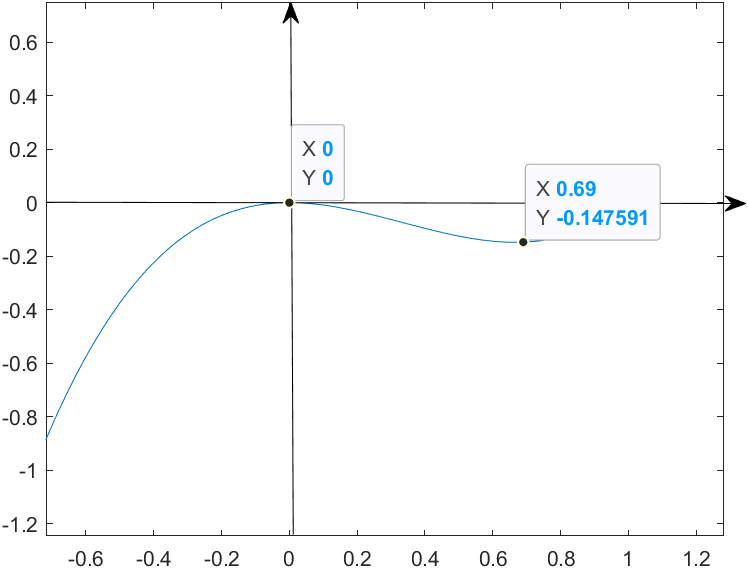
x = 0处,此时明显的,斜率应该为0,二阶导数为-2,此时二阶导数表示,图像向下弯曲,即凸。因此,此处是极大值而不是极小值。
另一个极值点,x = 2/3处,斜率为0,二阶导数为2,此时二阶导数表示图像向上弯曲,即凹,因此此处是极小值点。当然它也不是最小值,导数只能解释点周围很小很小范围内(领域内)的情况,这一点的导数无法连接,函数左会无限下降,函数右会无限上升。
知道函数后就能求出极大值点和极小值点,但最好还能找到拐点(弯曲方向变化的分界点)。
令二阶导数为0,或者通过图像,得出当x = 1/3的时候,这是一个拐点。
现在,就基本上找齐了函数上的所有特殊点,这些点其实都是有实际意义的。
假设你是一个经济学家,你正在分析某个地区的经济统计数据,你发现曲线的斜率一直为负,即经济一直在不断的下降,但是突然你发现近两年有经济复苏的现象,因为此时的图像向上弯曲,即二阶导数为正,数据虽然继续下降,但是速度开始变慢,在某一点上,到达最低点,触底反弹,一定是拐点后某一点。
极值点,可以说是导数最重要的应用之一,设导数为0,找到极大值和极小值点,微积分里大多数应用问题都要令导数等于0。
指数函数
y = ex
这种函数用代数的方法无法建立,只有用微积分才能得到,因为要得到ex,要用到一些极限的步骤, 有些量趋于0,有些量趋于无穷。虽然有各种方法来得到e的x次方,但这些方法都会涉及极限的过程。
而对于极限
指数函数最重要的性质就是,指数函数的导数等于函数本身的常数倍,这就是指数函数与众不同的地方。
$$
\frac{d}{dx}a^x = a^x\ln a
$$
对于指数函数,y = dy / dx
这其实就是一个简单的微分方程,同时包含函数和函数导数。
首先,任何数的0次方都等于1,因此指数函数从1开始。
y(x) = 1
此时 dy /dx = 1
反推,y(x) = 1 +x时,导数为1。
为了确保微分方程相等,dy / dx = 1+x
此时,y(x)= 1 + x + x2/2
以此类推,好像让微分方程成立,即两者相等是不可能的,除非两个方程无限,这里也确实无限。
直接写出n次之后的结果
y(x) = 1+x+x2/2 + x3 / 3 * 2 + …. + xn/n(n-1)(n-2)…(1)+…
dy /dx = 1+x+x2/2 + x3 / 3 * 2 + …. + xn-1/(n-1)!+xn / n!+ …
简单的说,n!的增长速度太快了,远远超过了xn,因此实际上,在末尾的项,这些量会变得极其的小。这个级数会趋于一个极限,不会因为加了很多项而无限变大。
积分总览
一般地,我们说积分是与求导相逆的运算,也就是说这两个概念是相对的。
导数是函数变化率的一种度量,表示函数在某一点处的瞬时变化率;积分则是导数的逆运算,是在一段区间内的函数面积或曲线长度的计算,可以看作是对函数的累积求和。
其中关于面积的计算
对于一个函数 f(x),在区间 [a, b] 上的面积可以近似地用若干个矩形的面积之和来计算。
如果将区间 [a, b] 分成 n 个小区间,每个小区间的长度为
$$
\Delta x = \frac{b - a}{n}
$$
,则第 i 个小区间的左端点为
$$
x_i = a + i \Delta x
$$
,右端点为
$$
x_{i+1} = a + (i+1)\Delta x
$$
。在区间
$$
[x_i, x_{i+1}]
$$
上,可以用
$$
f(x_i)
$$
或者
$$
f(x_{i+1})
$$
来代表 f(x) 的值。因此,区间
$$
[x_i, x_{i+1}]
$$
上的矩形面积为
$$
f(x_i) \Delta x
$$
或者
$$
f(x_{i+1}) \Delta x
$$
。将所有小矩形的面积相加即可得到函数在区间 [a, b] 上的近似面积 :
$$
S \approx \sum_{i=0}^{n-1} f(x_i) \Delta x
$$
当 n 趋近于无穷大时,小矩形的宽度趋近于无穷小,可以得到函数在区间 [a, b] 上的确切面积 A:
$$
A = \lim_{n \to \infty} \sum_{i=0}^{n-1} f(x_i) \Delta x = \int_a^b f(x) dx
$$
其中,
$$
\int
$$
表示积分符号,dx表示对 x进行积分。
曲线长度的计算
曲线长度指的是一个平面曲线的长度,也被称为弧长。在微积分中,曲线长度的计算可以使用积分来实现。假设我们有一个函数
$$
y = f(x)
$$
,其定义域为区间 [a, b]。如果我们想要计算从 a到 b 的曲线长度,我们可以将曲线划分为许多小线段,每个小线段的长度可以用勾股定理求得。我们可以将每个小线段的长度相加,得到曲线的近似长度。为了得到更准确的结果,我们需要使用更小的线段来逼近曲线。将线段长度无限小的极限值称为弧长,可以用以下公式计算:
$$
L = \int_a^b \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx
$$
其中
$$
dy/dx
$$
表示函数在每个点处的导数。



