信息的表示与处理
信息的表示
二进制、八进制、十进制、十六进制。基数不同,只重位置,不看具体的值。
字长(指针的大小)
虚拟地址以此来编码,一般的高位机向后兼容。
计算机与编译器都支持多种的编码
无符号整数与有符号整数的区别在c中,关键字unsigned注明了无符号整数。
寻址与字节顺序
一般的,多字节对象连续存址。
机器之中排列字节地址有差异,有的以最低有效字节在前面——小端法,有的以最高有效字节在前面——大端法。
字符串表示:一般的字符串被编码以null结尾的字符数组,每个字符使用某种编码表示,例如ASCII编码。
布尔代数 0,1
布尔代数相关运算:与、或、非、异或。
布尔与:同位为1结果即为1,否则为0。
布尔或:同位有1结果即为1,否则为0。
布尔非:1为0,0为1。
布尔异或:同位为1但不同时为1为1,否则为0。
布尔代数—布尔环(w位向量上的与或非运算时的新形式)
位向量还可以用来表示掩码,i位为1时代表有效使能,为0则为无效使能。
C语言很号的支持按位布尔
位级运算实现掩码运算很好,这里的掩码表示一个位模式,表示一个字节中有效的位的集合。
逻辑运算
逻辑或、与、非。
非零的参数表示为TRUE,为0的表示为FALSE。
逻辑运算存在短路特性。
移位运算 向左或向右移动位模式
x << k 左移k位,丢弃最高的k位,在右端补齐k个0。
x >> k 右移k位,但是区分逻辑左移与算数左移的区分,对于逻辑右移,在左端补齐k个0,对于算数右移,需要补齐最高有效位,可能是1。
C没有规定有符号数应该使用哪一种右移,但是几乎所有的编译器都对有符号数采用算数右移,对于无符号数,右移必须是逻辑的。
在Java里,>>> 表示逻辑右移,>>表示算数右移。
优先级问题,移位的运算优先级低于加减法。
编码整数的方式又两种,一种只能表示非负数,一种都可以表示。
C中有多种数据类型,都可以表示整数:
CHAR、SHORT、INT、LONG(UNSIGNED)
他们表示的字节大小各不相同,一般的取决于字长,例如在32位机中,long只占4个字节。
无符号编码具有重要意义,因为这是一个双射。
原码、反码、补码
最高位为符号位,0表示正数,1表示负数。
正数的反码是自身,负数的反码是除符号位之外,全部取反。
正数的补码也是自身,负数的补码是反码+1
补码编码
补码:反码加一”只是补码所具有的一个性质,不能被定义成补码。负数的补码,是能够和其相反数相加通过溢出从而使计算机内计算结果变为0的二进制码。
用补码表示负数,在补码的定义之中,字的有效最高位解释为负权,因此最高位为1时,表示该数为负数。
对于补码而言,这也是一个双射,补码编码同样具有唯一性。
C语言标准之中没有要求使用补码来表示,有符号整数,但是几乎所有的机器都是使用补码的。
除却补码之外,原码与反码也能表示有符号整数。
原码、反码都以最高位为符号位,不同的是,反码符号位取非。
有符号数与无符号数之间转换
对C来说,类型的转换从不关心具体的数,对于这个问题,C是从位级角度来考虑的。
一般的,对于强制类型转换,位的值不发生改变,只改变位的位置。
零扩展
从较小的类型转换为较大类型时,在开头扩展0。
位截断
丢弃高位,可能会造成溢出。
有符号数到无符号数的隐式转换,会导致错误或者漏洞,杜绝的方式试试禁用无符号数。
例如:一种类型的表达式被赋值给另外一种类型的变量时,转换就是隐式的。
C语言中同时包含了对有符号和无符号数表达式的处理方式,当同时出现两种数时,C会隐式的强转为无符号数,例如在<,>运算中,结果就会很直观。
运算
无符号加法
考虑两个w位的无符号数相加,他们的和的范围应该在0到w+1位之间。
但是C不允许这样的扩张出现,因此必须使用过位截断,使得他们的和在0到w位之间。截断时,截断高位。
在C中,不会将溢出作为错误而返回信号。
溢出时,不难发现,结果等于两数之和与2
的w次方的模数。
补码加法
对于补码的加法,必须确定当结果太大(为正)或太小(为负)时,应该怎么做。
补码,最高位是符号位,表示负权。因此两个数的范围在-2w-1到2w-1之间。这意味着,要想表示两个数的和,需要w+1位。(符号位在内)
结果是截断到w位。
值得一提的是,两个数的w位补码之和和无符号数之和有完全相同的位级表示。
无符号乘法
对于两数乘积的取值范围,需要2w位来表示,明显的C语言不可能允许这样的大小扩张,最终结果依旧需要w位,而将无符号数截断为w位等价于计算该值取模2的w次方。
补码乘法
对于补码乘法,C语言的有符号乘法通过截断为w位来实现,将一个补码截断为w位,相当于先计算该值模2的w次方,再把无符号数转换为补码。
一般的,对于无符号和补码乘法来说,乘法运算结果的位级表示都是一样的。
例如:
(101) * (011) = (001111) = (111)【截断后的】
无符号数表示:5 * 3 = 7
(101) * (011) = (110111) = (111)【截断后的】
补码表示:-1 * 3 = -1
虽然完整的乘积的位级的表示可能不同,但是截断后乘积的位级表示是相同的。
乘以常数
因为,在大多数机器上,整数乘法指令相当的慢,需要10个或更多时钟周期,因此编译器进行了一项优化,试着用移位加加法运算的组合来代替乘以常数因子的乘法。
考虑乘以2的幂的情况,再推广至全体常数。
可以发现左移一个数值等价于执行一个与2的幂相乘的无符号乘法。固定大小的补码算数运算的位级操作与其无符号运算等价。
但是无论是无符号还是补码,乘以2的幂都会导致溢出,结果说明,即使溢出,通过移位得到的结果也是一样的。
除以2的幂
在大多数机器上,整数除法比整数乘法更慢,需要30或者更多的时钟周期。
除以2的幂,也可以用移位运算来实现,只不过使用的是右移,无符号数和补码分别使用逻辑移位和算术移位来达到目的。
整数除法总是舍入到0,它将向下舍入到一个正值,向下舍入到一个负值。
对于无符号运算右移很简单,一部分原因是因为无符号的右移一定是逻辑的。
c >> k产生的结果是 c / 2的k次方。
对于除以2的幂的补码运算来说,情况稍微要复杂一些,因为要保证负数依然为负,移位要执行的算数移位。
除以2的幂的补码除法,向下舍入
变量x和k分别有补码值x和无符号数值k,且0≤k<w,则当执行算术移位时,C表达式x>>k产生数值 x /2^k。
对于非负数来说,最高位是0,因此算数右移k位与除以2^k是一样的。
作为负数,如果出现舍入的情况时,移位导致结果向下舍入,此时就需要调整策略。
作为一个负数,算数右移后的位向量刚好就是就w-k位表示的补码数从w-k位符号扩展到w位。通过在移位之前,偏置这个值,来修正不合适的舍入。

思考:
计算机执行的“整数”运算实际上是一种模运算形式。
表示数字的有限字长限制了可能的值的取值范围,结果运算可能溢出。
补码表示提供了一种既能表示负数也能表示正数的灵活方法,同时使用了与执行无符号算术相同的位级实现,这些运算包括像加法、减法、乘法,甚至除法,无论运算数是以无符号形式还是以补码形式表示的,都有完全一样或者非常类似的位级行为。
浮点数
浮点表示对形如
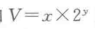
的有理数进行编码。它对执行涉及非常大的数字非常接近于0的数字,以及更普遍地作为实数运算的近似值的计算,是很有用的。
一般的,IEEE浮点标准被几乎所有的计算机支持。
二进制小数
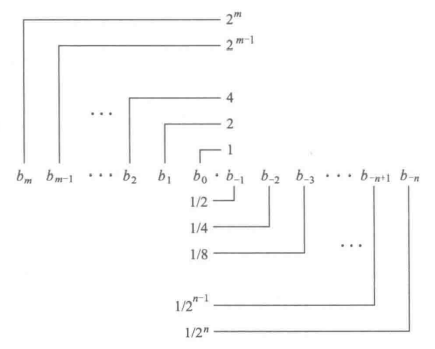
IEEE浮点表示
IEEE浮点标准用
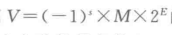
的形式来表示一个数:
符号(sign),s决定这数是负数(s=1)还是正数( s=0),而对于数值0的符号位解释作为特殊情况处理。
尾数(significand)M是一个二进制小数。
阶码(exponent)E的作用是对浮点数加权,这个权重是2的E次幂(可能是负数)。

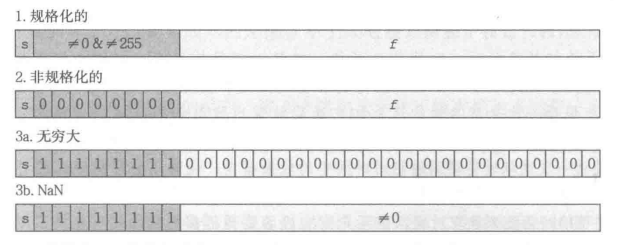
规格化
当exp的位模式不全为0,也不全为1时,都是规格化的。
阶码的值是E = e - 偏置值。
e是无符号数,偏置值为2的k-1次方-1,对于单精度是-126到127
小数字段frac被描述为小数值f,f在0到1之间。尾数的定义是M = 1+f。这种表示方法,假设没有一处,尾数在1到2之间,那么就能轻松额外获得一个精度位,既然第一位总是等于1,那么就不需要显示的表示它。
非规格化
当阶码全为0的时候,表示的书就是非规格化的。
阶码为E = 1 - 偏置,尾数M = f,也就是小数的值,不包含隐含的开头1。
非规格化数可以表示0,因为对于M来说,必须大于或等于1.因此不能表示0,事实上对于0的位模式,阶码字段与小数域全为0。
但是-0与+0在符号位上是有差异的,在IEEE中,在某些方面,他们被认为是不同的。
特殊值
当阶码全为1时,就会出现无穷的表示。
舍入
因为表示方法限制了浮点数的范围和精度,所有浮点运算只能近似的表示实数运算。
一般的,为了找到一个最接近的匹配值,可以用期望的浮点形式表示出来,这就是舍入。

浮点运算
IEEE标准指定了一个简单的规则,来确定加法和乘法这样的算术运算的结果。
C语言中的浮点数
C语言中提供了两种不同的浮点数据类型,float和double,在支持IEEE浮点格式的机器上,这些数据类型对应单精度和双精度浮点,另外这类机器采用偶数舍入的舍入方式。
当在int、float和 double格式之间进行强制类型转换时,程序改变数值和位模式的原则如下(假设int是32位的):
从int转换成float,数字不会溢出,但是可能被舍入。
从 int或float转换成double,因为double有更大的范围(也就是可表示值的范围),也有更高的精度(也就是有效位数),所以能够保留精确的数值。
从double转换成float,因为范围要小一些,所以值可能溢出成+∞或-∞。另外,由于精确度较小,它还可能被舍入。
从float或者double转换成int,值将会向零舍人。例如,1.999将被转换成1,而一1.999将被转换成一1。进一步来说,值可能会溢出。
C语言标准没有对这种情况指定固定的结果。与Intel兼容的微处理器指定位模式10…00为整数不确定(integer indefinite)值。一个从浮点数到整数的转换,如果不能为该浮点数找到一个合理的整数近似值,就会产生这样一个值。因此,表达式(int)+1e10会得到-21483648,即从一个正值变成了一个负值。



