计算机算术
数据是什么
各种各样的信息,数字、文本、程序、音乐、符号等。信息可以是能够被计算机存储和处理的任何事物。
位和字节
计算机存储和处理信息的最小单位是位(bit),一个比特表示0或1。
数字计算机将信息以一组或一串比特成为字保存在存储器中。
计算机通过高低电压来存储0或1。
计算机对一组二进制位进行操作,8个二进制位为一个字节(byte),一些计算机制造商用术语“字”表示16位的值,长字表示32位的值,还有一些制造商用字表示32位的值,用半字表示16位的值。
位模式
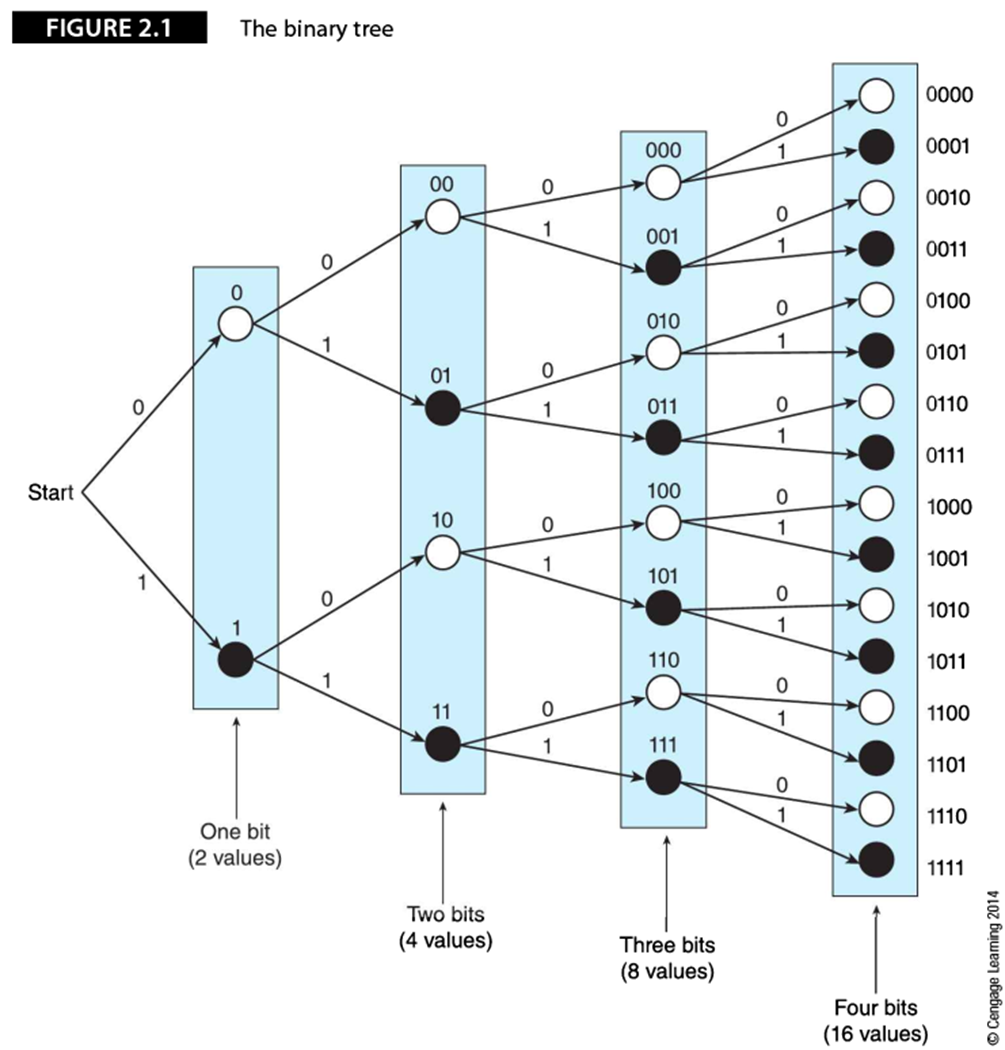
每当数字增加1位,路径的总数将翻一倍。一个n位的字将得到2n条不同路径或位模式。如,一个8位的字节将得到28=256个可能的值。
为了用二进制数表示任何一个拥有最多n个值的量,应找到一个使不等式n<=2m成立的最小位数m。
信息表示
一个n位的二进制什么也表示不了。因为一个由二进制1和0组成的串没有任何内在含义。需要程序员赋予它何种含义。
一个二进制串可以表示的对象有:
指令
字长为32位或更长的计算机用一个字来表示CPU能够完成的操作(8位或16位计算机用多个字表示一条指令)。指令的二进制编码与其功能之间的关系由计算机设计者决定。如,一台计算机上表示“A加B”的二进制序列可能与另一台计算机上的完全不同。
数量
一个字或多个字都可以用来表示数量。数可以被表示为多种格式,如有符号、无符号二进制整数、二进制浮点数、整数复数等等。
字符
字符是一个叫作“字母表”的集合中元素。拉丁或罗马字母表中的字母、数字字符(A-Z,a-z,0-9)和*、-、+、?等符号都被分配了二进制值,因此可以在计算机内存储和处理。
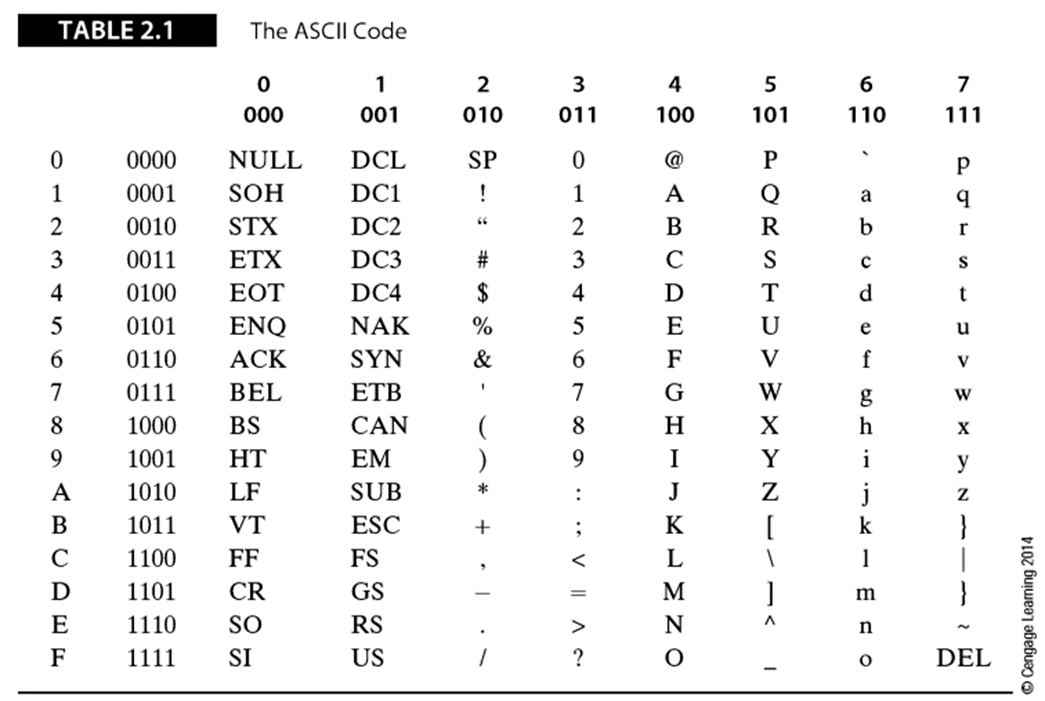
ASCII码表用7位表示一个字符,一共可以表示27=128个不同的字符。其中96个字符是可打印字符。其余32个是不可打印字符,用于完成回车、退格、换行等特殊功能。
扩展的ASCII码表:8位的ISO 8859-1拉丁编码。将7位的ISO/ASCII字符集扩展为8位,可以得到两个128个字符的字符集,如果字符的最高位为0,则其余7位代表128个标准ISO/ASCII字符中的一个,如果字符最高位为1,其余7位将表示128个新字符中的任意一个。
图像、声音和视觉
数字计算机处理大量表示声音、静态图像和视频的数据。
组成照片的基本单位是像素,每个像素的大小可以是8位(单色)或24位(三基)。
视频作为一串静态图像依次传输,每秒发送60次。
声音通过对波形信号采样。
无损压缩和有损压缩。
数字
用来计数的数字(即1,2,3,4…)被称作自然数。我们用十进制计数,因为它有0~9共10个符号。并非所有数字都是自然数,还有负数、实数等
现代数字系统中,使用位置记数法表示十进制数,每个数位的值或权取决于它在数字中的位置。
按照位置记数法,一个n位的整数N的形式表示:
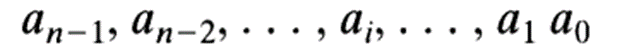
用小数点将整数部分和小数部分分开,可以对位置记数法进行扩展,使其能表示实数。
一个用基数b的位置记数法表示的数的值被定义为:
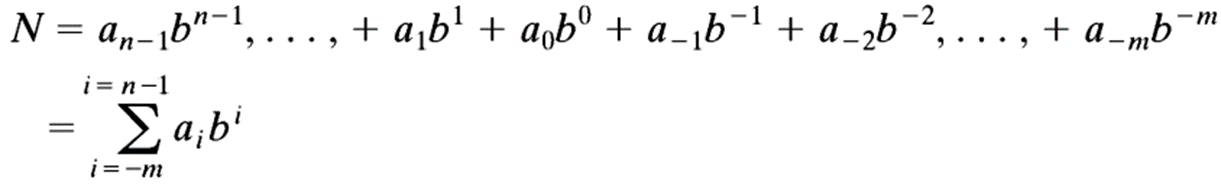
采用位置记数法,一个数的数值等于它各位值的总和,而每一位的值则是该位的数值乘以它在数中的位置所对应的权。
如:
十进制数1982 = 1 x 103 + 9 x 102 + 8 x 101 + 2 x 100
二进制数10110.11 = 1x24 + 0x23 + 1x22 + 1x21 + 0x20 + 1x2-1 + 1x2-2
十进制位置记数法不能精确表示所有小数,如1/3是0.3333333…33,二进制也是如此,如0.110 不能被精确转换为二进制形式。
二进制运算
二进制算术运算规则与十进制基本相同,区别是基数不同。

两个位相加可能产生进位或借位,和十进制运算规则相同。
下面描述了011010012(乘数)与010010012(被乘数)相乘的过程,两个n位字相乘将产生一个2n位的积:
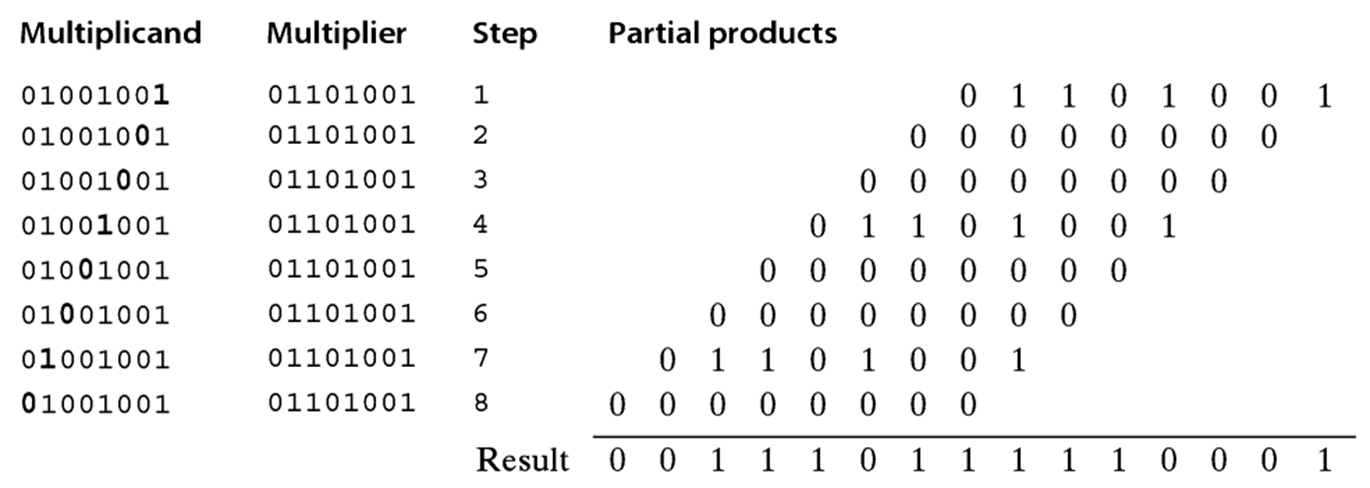
但是计算机并没有按照这种方式进行计算。
有符号整数
负数可以用多种不同的方式表示,计算机设计者选择了3种方法:符号及值表示法、二进制补码表示法、移码表示法,每种方法都有各自的优缺点。
符号及值表示法
一个n位字可以表示从0~2n-1共2n个可能的值。如,一个8位的字可以表示0,1,…,254,255。表示负数的方法是用它的最高位表示符号,通常符号位为0表示正数,符号位为1表示负数。
下面两个8位有符号二进制00001101和10001101的值为:

n位有符号的表示范围为-(2n-1-1) ~ +(2n-1-1)。一个8位有符号数的表示-127(11111111)~ +127(01111111)之间的整数。
有人反对该系统的一个原因是它有两个值都表示0:
00000000 = +0 和 10000000 = -0
符号及值表示法没有被用于整数算术运算中,因为它的加、减法运行需要分别用加法器和减法器实现。符号及值表示法用于浮点算术运算中。
二进制补码运算
微处理器用二进制补码系统表示有符号整数,它可以将减法运算转换为对减数的补码的加法运算。
一个数与它的补码之和是一个常数。如,一个一位十进制数与它的补码之和总是9。2的补码是7,因为2+7=9。在n位二进制算术中,数P的补码为Q且P+Q=2n。
在二进制算术中,求一个数的补码的方法是将其各位取反并加1。
如:01100101的补码为10011010+1=10011011。
一个n位二进制数N的二进制补码定义为2n-N。如果N=5=00000101(8位二进制数),则N的补码为28-00000101=100000000-00000101=11111011
下面说明了8位二进制数的补码运算过程,将4个数+5、-5、+7、-7转换为补码:

将7与5的补码相加:
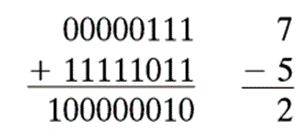
结果为9位二进制数100000010。如果忽略最左边一位(进位位),结果为000000102=+2,正是希望得到的结果。
将-7加5:

结果为11111110(进位位为0)。也是希望得到的结果-2,即28-2=100000000-00000010=11111110
n位二进制算术运算Z=X-Y,用X加上Y的补码完成运算:Y的补码为2n-Y,则Z=X+(2n-Y)=2n+(X-Y)。我们得到了需要的结果,X-Y,以及位于最左边的一个并不需要的进位(即2n),而这个进位被丢弃了。
一个数两次求补码得到该数本身。如-5=28-00000101=11111011。
即-x=2n-x且-(-x)=2n-(2n-x)=x。

求补运算
一个n位的二进制数N的补码,被定义为2n-N,则
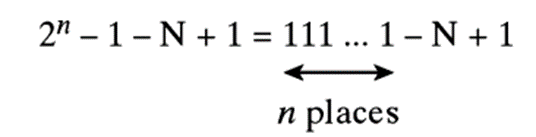
如,8位(n=8)时有:
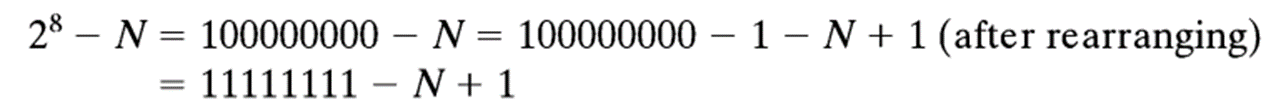
表达式11111111-N的值很容易计算,对N的第i位ni,若ni=0,则1-0=1,若ni=1,则1-1=0。显然:
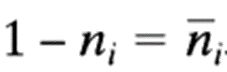
所以计算N的补码就是将N的每一位取反加1。
之所以使用这种求补码的方式,是因为在硬件上它十分容易实现。
补码的特点
补码互补因为X+-X = 0
补码被表示为000….000,是唯一的
补码的最高位为符号位,符号位为0,则该数为正,符号位为1,该数位负。
n位二进制位的补码表示范围为-2n-1—2n+1,对于8位,是-127-128。
补码的加减法使用同样的硬件完成,因为补码的减法由被减数的补码实现。
运算溢出
溢出的问题,主要是补码表示范围的限制。如果两个数运算后结果的值不在范围内,那么就会溢出,并且如果操作数的两个符号位相同,但是结果的符号位与他们不同,同样也会发生溢出。
乘除法
计算机必须实现乘除法,但是相对来说,这比加减法要复杂的多。
移位运算
首先是二进制的算术移位运算,进行移位运算时,一个数的所有位都会向左或者向右移动n位,有些计算机可以一次移动多个位。
二进制补码正数左移移位等于乘2。(正数的补码原码反码一致)
算术左移:最低位补0,最高位被复制到进位标志中,如11000101左移一位得到10001010
算术右移:最高位补符号位,所有位右移一位。最低位复制到进位标志中。如00100101右移一位得到00010010。11100101右移一位得到11110010。
二进制右移一位相当于除以2。
无符号二进制乘法
计算机从乘数的最低位开始,每次检查一位,判断它是否为0,如果乘数的当前位为1则写下被乘数,若该位为0则写下n个0。接下来检查乘数的下一位,这时应从上一位数的左边一位开始写下被乘数或0。被写下的这一组数叫作部分积。得到所有的部分积后,加到一起,得到乘法结果:

两个二进制数相乘得到一个2n位的积。
但是计算机并没有实现上面的算法,这种算法要求计算机存储n个部分积,然后将它们同时相加。更好的做法是每得到一个部分积就做一次加法。
下面给出了一个计算两个n位无符号二进制数相乘的算法:
步骤a:将计数器的值置为n
步骤b:将2n位的部分积寄存器清零
步骤c:检查乘数的最右位(即最低位),将被乘数与部分积的最低位n位相加
步骤d:将部分积右移一位
步骤e:将乘数右移一位(乘数的最右位被丢弃)
步骤f:将计数器的值减1,重复步骤c直到n个周期后计数器的值变为0。部分积寄存器的内容就是乘积结果。
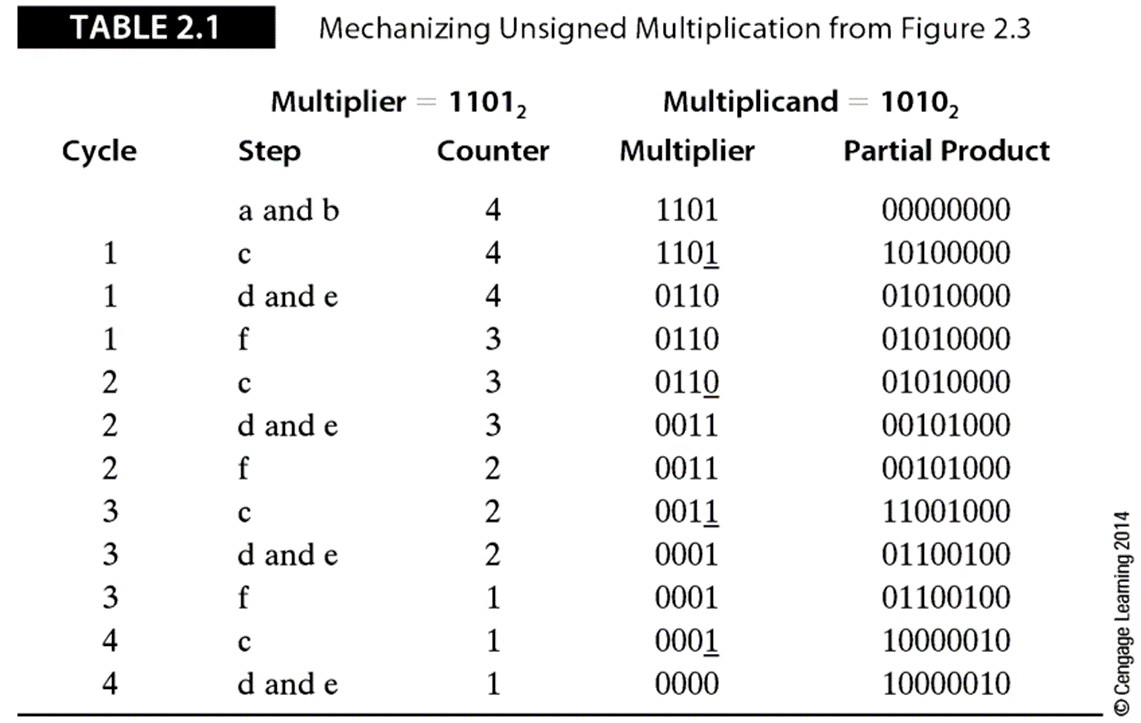
快速乘法
通过移位和加法实现的乘法速度很慢,实际的计算机采用了多种方法加快乘法运算的速度。
有些程序员使用移位和加法等速度相对较快的操作避免使用乘法。
考虑P乘以10和P乘以9的两个例子:
10P= 2x(2x2xP+P) ,即将P左移2次,加上P,再将和左移一次
9P= 2x2x2xP + P,即将P左移3次,加上P得到结果
乘法运算也可以借助查找表(look-up table)实现,这种方法将两个数相乘所有可能的积都保存在一个只读存储器内。这样只需简单的用X和Y的值找到表中的对应项就可以得到X和Y的乘积。如,两个8位二进制乘法需要一个16位地址、216项的查找表,每项记录一个16位的积。
缺点:太占空间了。
可以用一个简单方法来减少查找表的大小:假设计算两个16位数A与B的乘积,可以将16位数A拆分为两个8位数Au和Al,Au是A的高8位,Al是A的低8位。如
果A=1111000010101010,则Au=11110000,Al=10101010。A可被表示为Au x 256+Al,B可被表示为Bu x 256+Bl,则
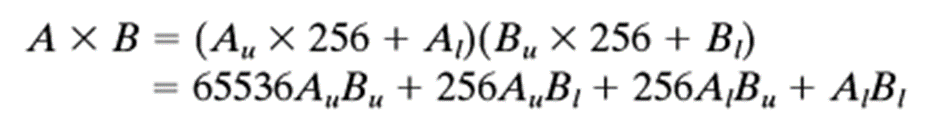
这样可以用8位乘法和4个加法来完成16位乘法。
除法
除法是通过被除数不断地减去除数直到结果为0或小于除数来实现的。减去除数的次数称作商,最后一次减法的差称作余数。
被除数/除数 = 商 + 余数/除数
下面描述了575除以25的过程:
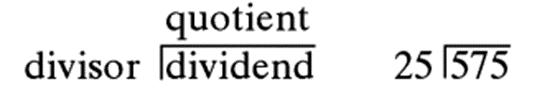
将被除数的下一个数字5移到7的后面,并比较除数和75,由于75正好是25的整数倍,因此在商的下一位上写下3:
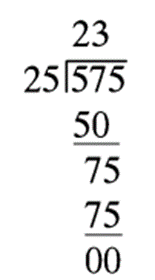
因为已经处理到被除数的最后一位且75正好是测试的整数倍。除法结束,商为23,余数为0。
考虑用无符号二进制除法完成同样的例子:
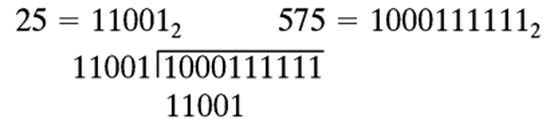
被除数的前5位比除数小,因此商的最高位为0并将除数与被除数的前6位比较
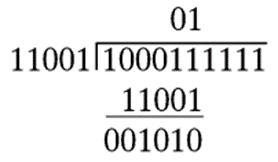
被除数的前6位中有一个除数,减法后得到新的部分被除数为001010(1111),将被除数的下一位移下来

新的部分被除数小于除数,因此商的下一位为0,后续除法过程如下:

除法结果商为10111,余数为0。
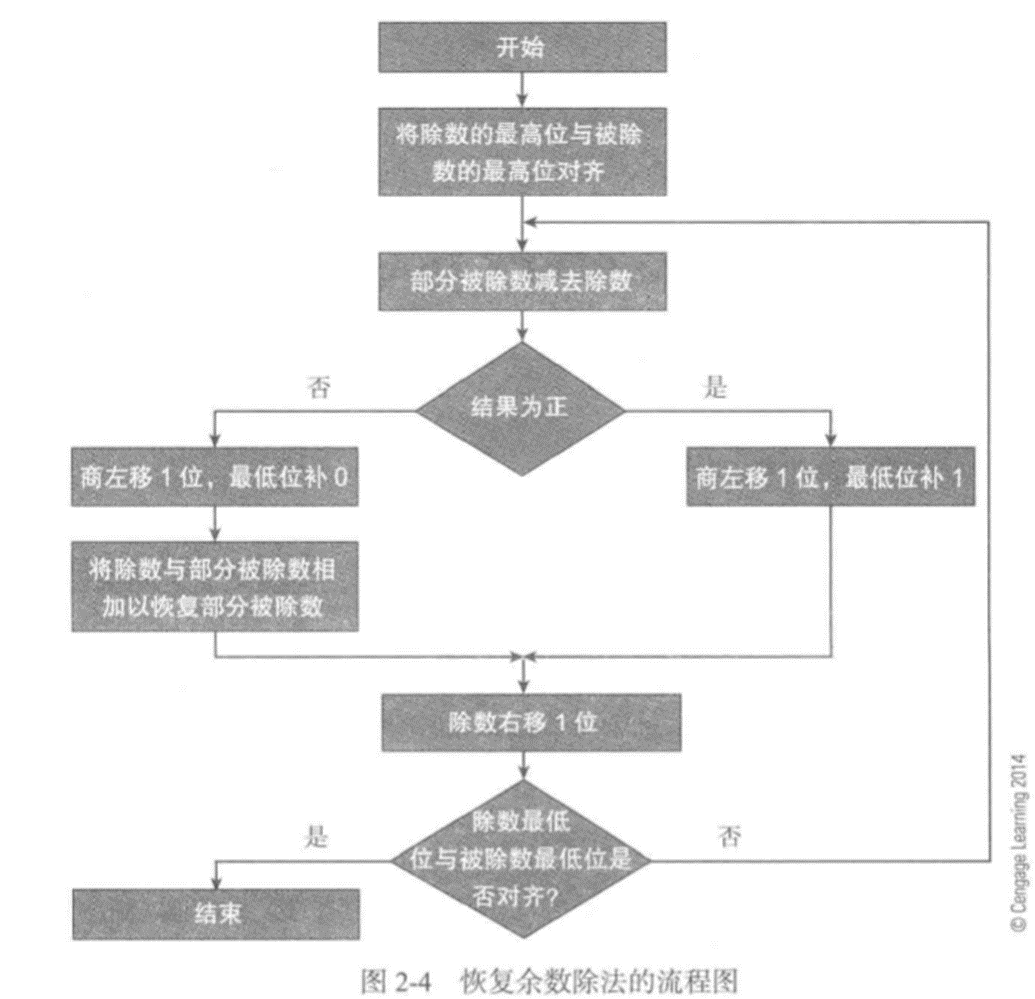
恢复余数除法
刚刚讨论的除法方法,用计算机实现,需要修改的就是除数与部分被除数的比较方法,计算机减去并检测结果的符号位。如果减法的结果为正,则商1,如果结果为负,则商0并将部分被除数与除数相加,将其恢复为原先的值。
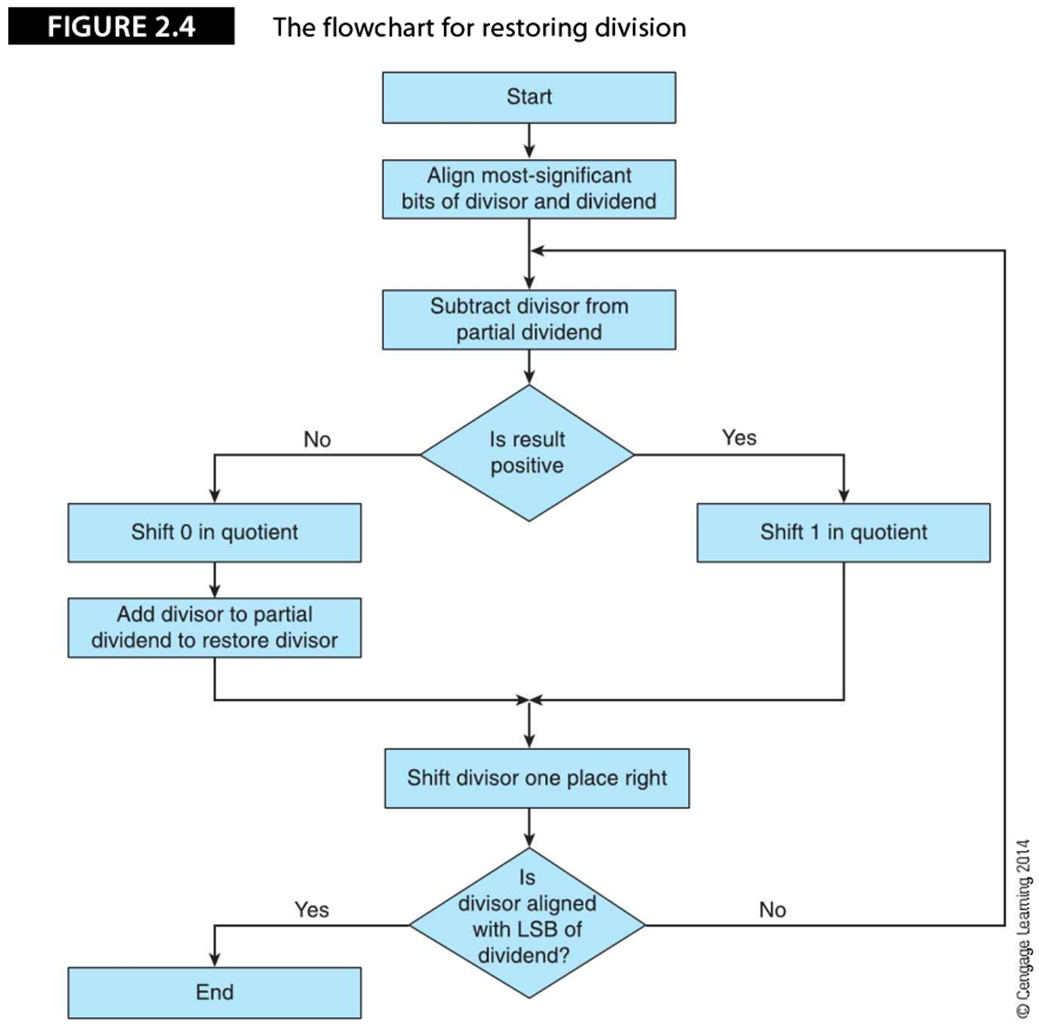
恢复余数除法算法:
1)将除数的最高位与被除数的最高位对齐
2)从部分被除数中减去除数,得到新的部分被除数
3)如果新的部分被除数为负数,则商0并用新的部分被除数加上除数,恢复原先的部分被除数
4)如果新的部分被除数为正,则商1
5)判断除法是否结束,如果除数的最低位与部分被除数的最低位对齐,则除法结束,最后的部分被除数就是余数。否则,执行第6步
6)将除数右移一位,从第2步继续执行
不恢复余数除法
不恢复余数除法与恢复余数除法基本相同,唯一区别在于取消了恢复余数的操作。
在恢复余数除法中,在部分被除数与除数相加恢复部分被除数之后的一个周期,部分被除数将减去除数的二分之一。每个将除数右移的操作等价于将除数除以2。当前周期恢复部分被除数以及下个周期减去除数一半的操作等价于部分被除数加上除数的一半。即D – D/2 = +D/2,D为除数。
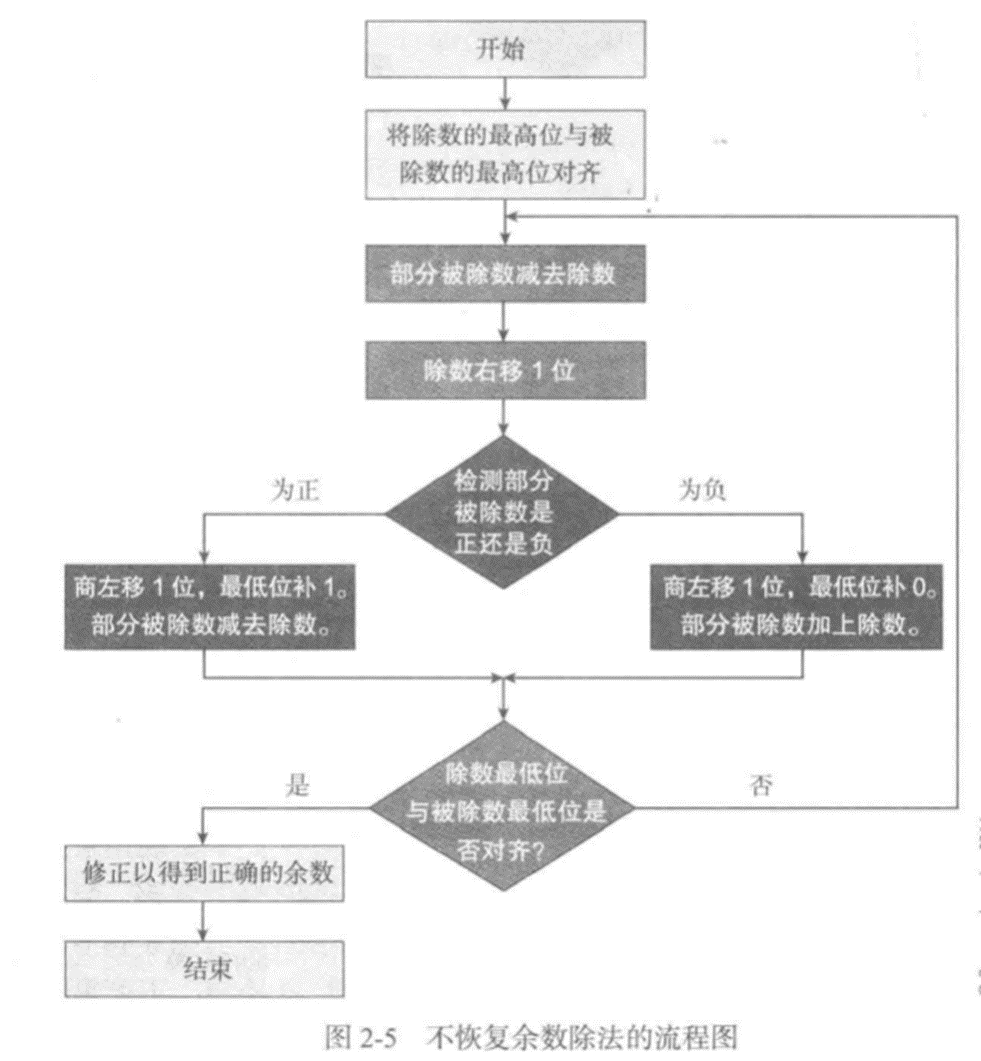
部分被除数减去除数之后,将检测新的部分被除数的符号位。若为负,则商左移1位,商的最低位补0,并将部分被除数加上除数的二分之一。若为正,则商左移1位,商的最低位补1,并将部分被除数减去除数的二分之一。
浮点数
浮点数即实数,实数是所有有理数和无理数的集合。
之所以叫作浮点数,是因为小数点在数中的位置并不是固定的。一个浮点数值分为两部分存储 :数值以及小数点在数值中的位置。
计算机中的浮点运算的计算结果一般是不确定的,一块芯片上的浮点计算结果也许与另一块芯片上的不同。
科学计数法:来表示很大或很小的数。
十进制浮点数可以被表示为:尾数x10指数,如1.2345x1020
二进制浮点数可以被表示为:尾数x2指数,如1.0111x25
IEEE 754浮点数标准提供3种浮点数表示:32位单精度浮点数、64位双精度浮点数、128位四精度浮点数
IEEE 754浮点数的尾数总是规格化的,其范围为1.000…0x2e到1.111…1x2e,e为指数。
规格化浮点数的最高位总是1,规格化使尾数的所有位都是有效的,因而尾数精度最高。
如:
0.10…x2e规格化为1.10…x2e-1
10.1…2e规格化为1.01…x2e+1
尾数规格化充分利用了可用的最大精度。如,一个8位非规格化的尾数0.0000101只能有4位有效位,而规格化后的8位尾数1.0100011则有8位有效位。
IEEE 754浮点数的尾数被表示为符号及值的形式,即用一个符号位表示它是正数还是负数。它的指数则用偏置方式表示,即给真正的指数加上一个常数。
假定所用的指数为8位,偏置值为127。如果一个数的指数为0,则被保存为0 + 127=127。如果指数为-2,则被保存为-2 + 127 = 125。
实数1010.1111规格化的结果为+1.010111x23,指数为+3,将被保存为3+127=130,即13010用二进制表示为10000010。
这种用偏置表示指数的方法优点在于,最小的负指数被表示为0,如果不采用这种方法,0的浮点表示为0.0…0x2最小负指数。采用偏置指数,0就可以用尾数0和指数0表示:
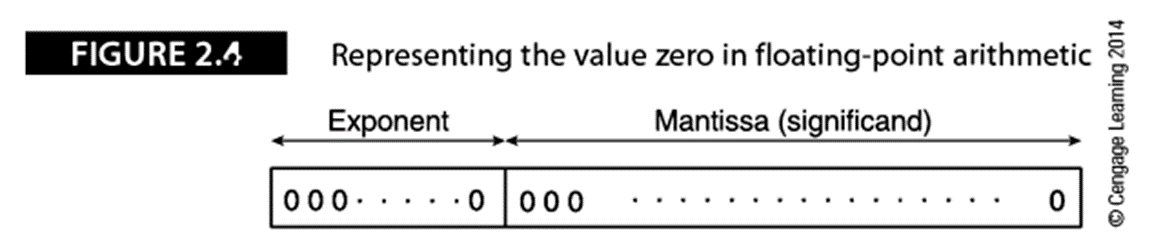
一个32位IEEE 754单精度浮点数可以被表示为下面的二进制串:
S EEEEEEEE 1.MMMMMMMMMMMMMMMMMMMMMMM
S为符号位,指明这个数是正数还是负数
E为8位偏置指数,指出了小数点的位置
M为23位尾数
下图描述了32位浮点数的结构:

S位为符号位,决定了数的符号,若S=0,则为正数,若S=1,则为负数。
指数E将浮点数的尾数扩大或缩小2E倍,并且偏置值为127。
如浮点数+1.11001…0x212的指数为12+127=13910=100010112 。
IEEE浮点数的尾数总是规格化的,其值范围在1.0000..00~1.1111..11,除非这个浮点数是0,此时尾数为0.000..00。
由于尾数总是规格化的,且最高位总是为1,因此将尾数存入存储器时没有必要保存最高位的1。所以,一个非0的IEEE 754浮点数可被定义为:
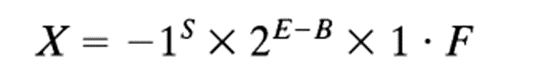
S:符号位
E:偏置量为B的指数
F:尾数的小数部分(实际的尾数为1.F,有个隐含的1)
浮点数0被表示为S=0,E=0,M=0(即浮点数0用全0表示)
浮点运算
浮点数不能直接相加。
下面以一个简单的8位尾数和一个未对齐的指数为例说明浮点运算,A=1.0101001x24,
B=1.1001100x23。若要计算两个数的乘积,应将尾数相乘,指数相加:
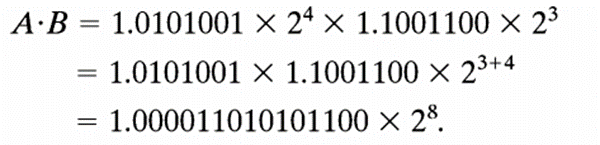
由于浮点操作数已被表示为规格化形式,计算机在进行浮点加法时面临以下问题:
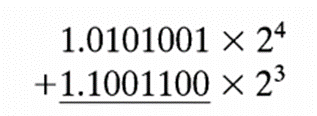
为了对齐指数,计算机必须执行下面步骤:
第1步,找出指数较小的数
第2步,使两个数的指数相同
第3步,尾数相加(或相减)
第4步,如果有必要,将结果规格化
因为B的指数比A小,将B转为0.110011x24,将A与非规格化的B相加:

对结果规格化,得到1.00001111x25
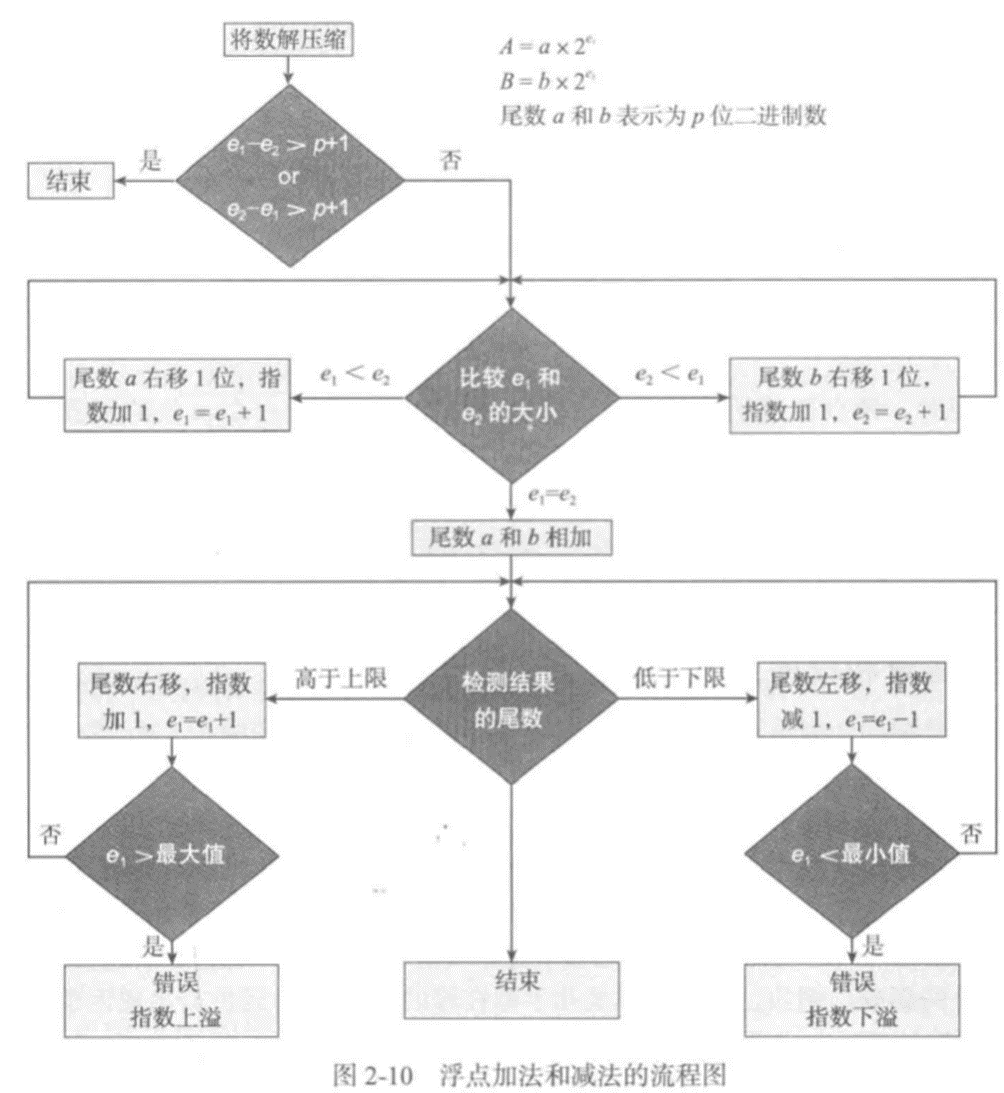
注意:
1)因为指数有时与尾数位于同一个字中,在加法过程开始之前必须将它们分离开(减压缩)
2)如果两个指数的差大于p+1,p为尾数的位数,较小的数由于太小而无法影响较大的数,结果实际就等于较大的数。如,1.1010x260+1.01x2-12的结果为1.1010x260,因为指数之差为72
3)结果规格化时检查指数范围,以分别检测指数下溢或上溢。指数下溢会导致结果为0,而指数上溢会造成错误。
舍入和截断误差
浮点运算可能引起尾数位数的相加,需要保持尾数位数不变的方法。最简单的技术叫作截断。
如,将0.1101101截断为4位尾数的结果为0.1101。截断会产生诱导误差(即误差是由施加在数上的操作计算所引起的),诱导误差是偏置的,因为截断后的数总比截断前小。
舍入是一种更好的减少数的位数的技术。如果丢弃的位的值大于剩余数最低位的一半,将剩余数的最低位加1。
考虑两个数在小数点后第4位上舍入的例子:
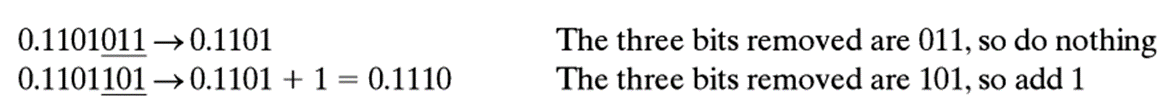
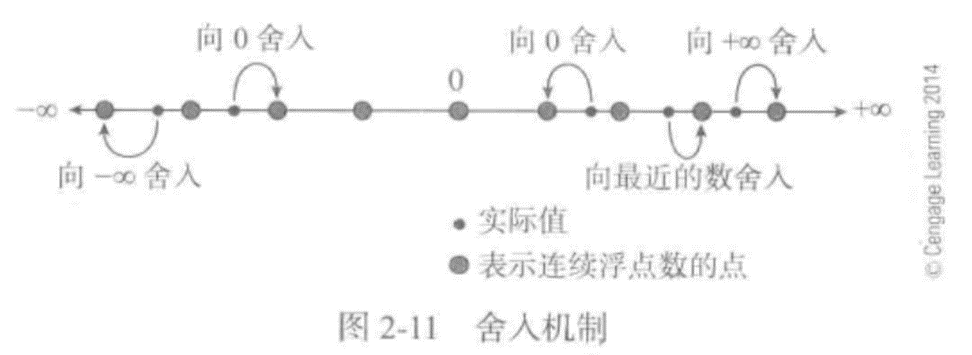
1)最简单的舍入机制是截断或向0舍入。
2)“向最近的数舍入”方法会选择距离该数最近的那个浮点数作为结果。
3)“向正或负无穷大舍入”方法会选择正或负无穷大方向上最近的有效浮点数作为结果。
当要舍入的数位于两个连续浮点数的正中时,IEEE舍入机制选择最低位为0的点(即向偶数舍入)。
整数操作时精确、可重复的,浮点数操作是不精确的。
考虑表达式z = x2-y2,x、y、z都是实数。可以将表达式视作x2-y2或(x+y)(x-y)计算,整数运算得到相同结果,但浮点数运算可能得到不同结果。
IEEE要求加、减、乘和除运算结果能够精确计算,并用向偶数舍入的方法将结
果舍入为最近的浮点数。




