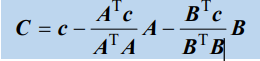开端是矩阵
线性方程组
向量集
矩阵
这就是线性代数,当然如果你足够具有空间思维,你会发现如果这个方程组有唯一解,此时的A向量集中的三个向量应该可以通过线性组合成一个完整的三维空间。
数乘与加减构成线性组合。
线性组合的对象不是变量而是向量。
如上,这就是一个二维的列向量。
向量加法,此刻v与w的第一与第二分量依然要分开。
这是纯量乘法,当然一般叫数乘,依然是数字乘每一个分量。
结合向量加法与数乘的结果就是线性组合。
向量加法(头到尾),v的终点就是w的起点。

如果此时方程组有唯一解,对于这个三元一次方程组而言,有唯一解就意味着所有的方程都有作用,不存在无意义的方程。
这一类无意义的方程例如是
逆矩阵
此处讨论的所有矩阵(n阶方阵)
不是所有的矩阵都可逆。
矩阵可逆,演绎法上通过消元法来确认矩阵A必须具有n个非零的主元,也就是说矩阵的秩,或者说构成向量空间的维数必须等于n。
代数法是行列式,矩阵可逆则行列式不可为0。此处可以使用化上三角或者下三角的方式,将矩阵变成三角矩阵,此时行列式的值特殊在,主对角线上包含了一个行列式的展开式形式,当行列式为0时,行列式的最后一行是全零行,此时矩阵的最后一行不是必要的,矩阵不是满秩的,因此不可逆。
方程式也可以测试可逆的性质,Ax=0,x=0必须是唯一解时,矩阵是可逆的。
如果A,B都可逆(相同的大小),那么AB,BA都是可逆的。
如何得到逆矩阵?
高斯若尔当消元。
奇异
如果A不可逆呢?那么他就是奇异的。
奇异矩阵,指的是列相关,当然行也肯定相关的矩阵,不难得出此时矩阵的行列式为0,并且轻易的能得出不可逆的性质。
从方程式上看,Ax=0,应该具备有无穷多解,Ax=b无解或者具备无穷多解。毕竟这样奇异的矩阵写成方程组相当于,n个未知数但是有效的方程不到n个。
秩数上来看,A的秩明显小是于n。
此时再简化行阶梯型,那么至少存在一个全零行。
再看列空间的维度,明显小于n,行空间同理。
特征值呢?0是A的一个特征值
正定性?只有半定。
奇异值?A有r<n个奇异值
正交
两个二维空间上的向量正交或者是三维上的,很好理解,就是垂直,此时向量的点积为0。
这里来讨论正交子空间与正交基底以及正交矩阵。来为矩阵正交化铺垫。
矩阵的子空间指的是,Ax = b的行空间与列空间以及Ax = 0的零空间与的零空间。
A的列空间,A矩阵中所有列向量构成的向量空间。
行空间垂直于A的零空间,列空间垂直于A的转置的零空间。
行空间与零空间垂直,A 的每个行与Ax = 0 的每个解垂直,得到图形左侧的90度角。
列空间与 A T 的零空间垂直,当 b 在列空间之外,当我们想要求解 Ax = b 却 做不到时,此时 A的转置的零空间就会显示出独特的优势,它包含“最小二乘”解的 误差 e = b - Ax,最小二乘是线性代数在本章中的关键应用。
行与列空间有相同的维度 r (他们吸取相同大小),两个零空间有剩下的维度n - r与m - r。现在我们证明行空间与零空间是向量空间中的正交子空间。
A 的行不可能在 A 的零空间中 (除了零行之外),两个正交子空间中都存在的向量只有零向量。
投影
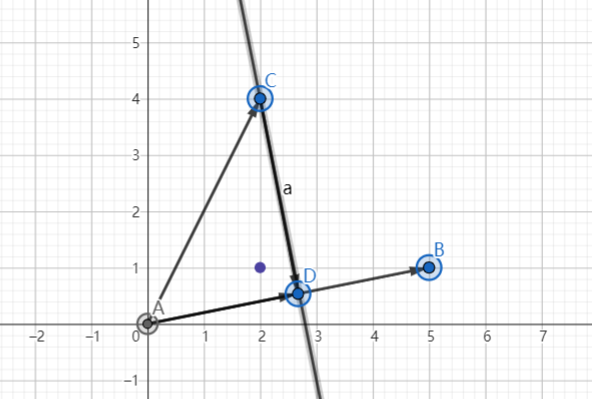
如图所示,ac在ab上的投影ad。cd与ab正交。
向量中,求解ad很容易。
矩阵也是一样的思路,只是我无法用几何的方式展示而已。
正交单位基底与格莱姆-施密特
若 Q 也是方形,则 Q Q的转置= I 且 Q 的转置 = Q 的逆矩阵,Q 是“正交矩阵”。